
Computación para Astronomía
y Meteorología
Lenguaje Fortran
Apuntes de Clase
Carlos Feinstein
Cátedra de Computación
Facultad de Ciencias Astronómicas y Geofisicas
UNLP
Versión del 2024-09-01
Estos apuntes tienen como fin ser el soporte para consultas de los
alumnos de las carreras de Astronomía y Geofísica en la Facultad1 en los temas de la asignatura
Computación en el área de la programación en lenguaje Fortran. En esos
apuntes haremos énfasis en la Versión de Fortran 77 aunque al final de
cada capítulo encontrarán referencias a modificaciones que pueden haber
tenido las distintas órdenes en la versión de Fortran 90/95. Si bien
este último tiene varias funcionalidades que lo hacen más versátil
también es algo más complejo y su aprendizaje necesitaría más tiempo del
que se dispone por la duración del curso.
Tenga en cuenta que en este apunte se usarán los términos programa y
código como sinónimos.
Todas las computadoras tienen una estructura en común aunque hayan
sido diseñadas con fines muy diferentes. Lo que puede cambiar entre
distintas computadora es la calidad y la tecnología de los componentes.
Los tiempos de respuesta de un sistema informático pueden ser más
rápidos con una mejor calidad de la electrónica, una mayor sofisticación
de los circuitos o la utilización de algoritmos más eficientes que
realicen la tarea a resolver en un tiempo menor. Por ejemplo, una
Playstation, un teléfono celular smartphone, una notebook, un televisor
(tipo smart-tv), una supercomputadora (que cuesta millones de dólares)
todos estos mecanismos son computadoras que comparten una estructura
común, aunque se usen para fines completamente diferentes. Normalmente
estamos más acostumbrados a las PC nombre que viene del inglés Personal
Computer, es decir computadora personal. Esta denominación las
diferenció en su aparición de los grandes sistemas que sólo se
encontraban en los centros de cómputos de universidades o
empresas.
Lo primero que tenemos que diferenciar son las dos
estructuras constructivas principales que hacen funcionar una
computadora. Estas son el HARDWARE y el SOFTWARE
Veremos ahora lo que son cada una de estas estructuras:
Hardware: Si lo traducimos del inglés así como palabra
de uso común esta sería ferretería (si, ese lugar al que iríamos a
comprar tornillos o tuercas) y no es una mala traducción. Hardware es
toda la estructura de circuitos electrónicos de la computadora,
incluyendo soporte y ventilación. Dicho de otro modo, es lo que podemos
tocar en una de estás máquinas, es tangible, está ahí. Los que diseñan y
construyen hardware suelen estudiar en las facultades o departamentos de
ingeniería.
Software: El software es algo intangible pero real.
Engloba a las instrucciones que se le dan a una computadora para que
ejecute, y de esta manera, que produzca los resultados que se desea.
Sería el equivalente a los algoritmos que se estudian en álgebra, pero
ahora implementados en el sistema de computación. Ustedes ya conocen
diferentes tipos de Software, por ejemplo, los Sistemas Operativos (SO):
En un celular pueden ser el Android o el IOS, o en una PC podrían ser
Windows (realizado por Microsoft), MacOSX (programado por Apple) o el
que usaremos en la práctica: el LINUX. Este último fue desarrollado por
voluntarios de Universidades y de empresas por todo el planeta. Sobre
estos SO corren los programas cuyas órdenes fueron escritas en lenguajes
de computación. En esta cursada vamos a darles los elementos necesarios
para desarrollar software de cálculo matemático, de visualización y
análisis de datos, utilizando dos lenguajes el FORTRAN y el
PYTHON.
Los que trabajan en desarrollo de Software estudian en facultades de
informática o sistemas.
La CPU (iniciales en inglés de Central Processing
Unit o Unidad de Procesamiento Central) es el componente de la
computadora que realmente realiza el trabajo. En la actualidad es un
chip (o un conjunto de varios chips dentro del mismo encapsulamiento y
que interactúan en conjunto). Este circuito electrónico está construido
con el equivalente a millones de transistores y es una de las partes más
caras de la computadora. Cada elemento electrónico tiene tamaños de 5 a
14 nm (nm es un nanómetro cuyo tamaño es \(10^{-9}\) metros). En las computadoras
actuales este chip se instala sobre la placa madre (Motherboard). Las
CPUs no trabajan recibiendo órdenes en algo que se parezca a lenguaje
humano, las órdenes están en lenguaje binario. Las CPUs realizan las
operaciones que se indican en los programas y los cálculos matemáticos.
No poseen grandes cantidades de memoria.
En computadoras de uso profesional puede haber varias CPUs en la placa
madre y estas pueden realizar trabajo en paralelo. En esta situación
cada CPU realiza parte del trabajo al mismo tiempo, es como si se
construyera una casa y cada albañil construye una parte o un cuarto
diferente de esta. Entonces más albañiles permitirían construir la casa
en menos tiempo. Esto suele ser muy útil en los casos de cálculos
complejos donde se pueden hacer varias operaciones matemáticas a la vez.
Por lo cual, el trabajo se resuelve más rápido.
Muchas CPUs tienen estructuras para hacer paralelismo interno. A estas
estructuras que trabajan independientemente se las llama CORES, pudiendo
tener una CPU de una PC no muy sofisticada entre 4 y 8 cores como algo
estándar, pero hay CPUs que tienen más de 48 CORES. Además, en cada CORE
suele haber dos unidades de procesamiento matemático que se los denomina
Threads.
La CPU se relaciona con los demás componentes de la computadora en forma
sincrónica, es decir que todos los componentes
electrónicos reciben pulsos para realizar las operaciones de
transferencia de datos al mismo tiempo. Esto significa que cada
computadora tiene un reloj que crea esos pulsos. Recuerden que la
frecuencia como medida es la inversa del tiempo, es \(1/t\) y se mide en hertz. Un hertz es \([hertz] = [1/seg]\), por lo tanto, con más
Hertz (más pulsos por segundo), más rápida será la computadora para
correr un programa al funcionar todos sus elementos electrónicos a mayor
velocidad. Los valores actuales de los relojes que sincronizan las CPUs
están en los Gigahertz, es decir mil millones de pulsos por
segundo.
Para una explicación alternativa vea la figura 1.1. Un
problema asociado es que al aumentar la frecuencia del reloj aumenta
mucho la cantidad de calor generado, y por consiguiente, es un desafío
muy importante de las arquitecturas de las CPUs cómo eliminar o disipar
este aumento de temperatura. Por eso, se trabaja mucho en el diseño para
evitar generar calor por un lado y su disipación por el otro.
Otro aspecto del problema del calor está en el desarrollo de las CPUs
para notebooks y celulares, ya que si se desperdicia energía en generar
calor, la energía almacenada en la batería de estos sistemas se agotará
muy rápido. En este tipo de computadoras se prefieren entonces CPUs más
lentas para que la batería dure mucho más.
También existen las GPU (Graphics Processing Unit) que
usan para gráficas, tanto profesionales como para los juegos y son
apreciadas por los gamers. Pero tienen la competencia de las
NPU (Neural Processing Unit), que son circuitos
diseñados para acelerar los cálculos de los programas de inteligencia
artificial. Muchas cpus actualmente tiene dentro de ellas circuitos de
GPU y NPU. Las unidades de medida de las NPU son los TOPS, que indican
los Trillones de OPeraciones por Segundo que pueden realizar.

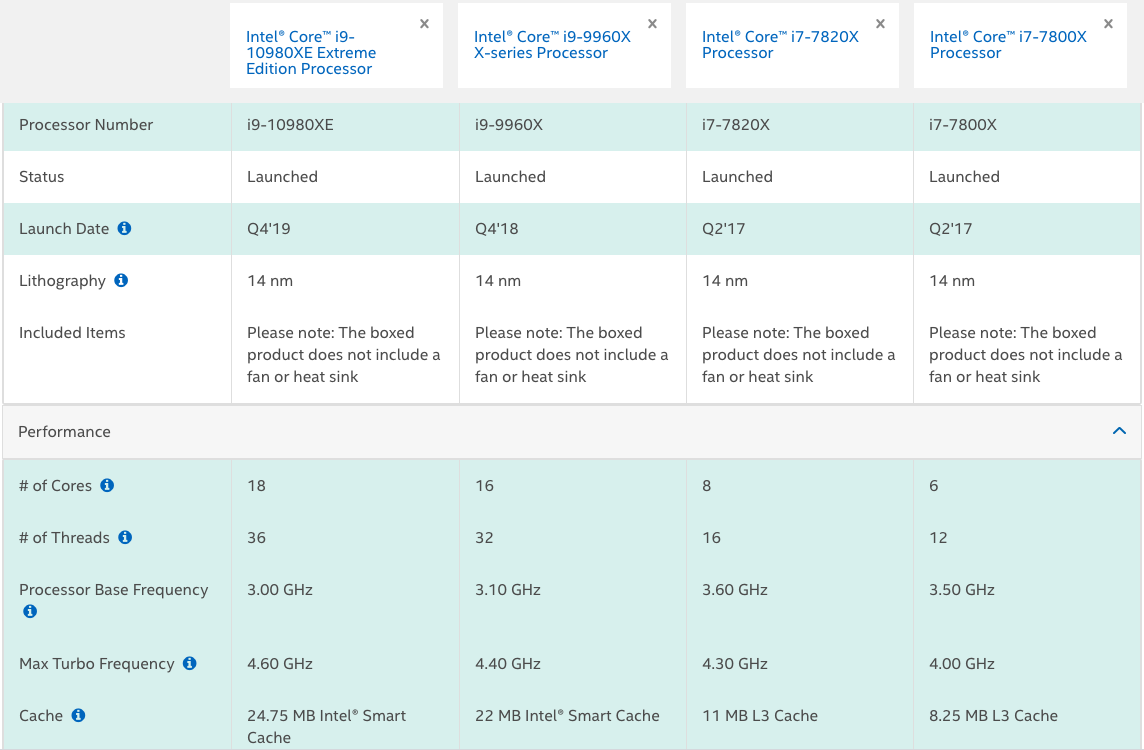
Veamos la siguiente publicidad de las empresas INTEL y AMD (figuras
1.2 y 1.3) que son los
mayores fabricantes de CPUs para las PCs (PC viene de Personal Computer,
es decir Computadora Personal).

La memoria RAM, cuyo nombre proviene del inglés Random Access Memory
(memoria de acceso aleatorio), es la memoria en donde se guardan los
programas que están corriendo en la computadora y sus datos. Esta
memoria funciona siempre que la computadora esté encendida. Un corte de
corriente haría que los datos que están guardados en esta memoria se
pierdan. La CPU se conecta con la memoria con un sistema de cables que
se los denomina Bus de datos.
Existen en general dos tipos de esta memoria, la
Dinámica y la Estática. La primera es
de muy bajo costo de fabricación y con capacidad de ser accedida en
algunas decenas de nanosegundos (recordar que un nanosegundo es \([ns]=10^{-9}\) de segundo), claramente en
un tiempo fuera de la escala de la percepción humana. Esta memoria tiene
la desventaja que necesita ser recargada de energía en períodos cortos
de tiempo, y entonces, la computadora pierde tiempo en esta tarea. Por
otro lado, la memoria Estática es mucho más rápida (del
orden de algunos ns) y no tiene que ser recargada, pero su precio es
mucho más alto y encarece a la computadora.
Para que las computadoras funcionen más rápido y su costo de fabricación
no sea muy alto, se usan ambas memorias en combinación. De esta forma se
usa memoria dinámica en grandes cantidades (que es muy barata), pero en
el camino del Bus de datos se encuentra un sistema de memoria estática
(no mucha, por su precio) que guarda lo último que haya pasado por este
Bus. Es decir, si guardo un número de un cálculo en la memoria, este se
copia en la memoria estática en el camino a guardarse en la dinámica. A
esta memoria en el camino se la llama memoria CACHE.
Las CPUs modernas suelen tener memorias cache dentro de ellas para ganar
tiempo. Estas trabajan adelantando datos que hace poco se hayan usado y
que estén ahí en vez de tener que ir a buscar a ese dato particular a la
memoria dinámica. Las CPUs modernas tienen varios niveles de cache
interno, incluso algunos cores dentro de la CPU tienen sus propia
memoria cache.
Es una clase de memoria que se graba los datos y quedan en forma
permanente, aún con la computadora apagada. ROM es la sigla de Read Only
Memory, que significa que es una memoria que sólo se puede leer. La
información que está en la ROM fue puesta por el fabricante de la
computadora. En este tipo de memoria suele estar un software llamado
BIOS que es el que corre cuando arranca la computadora y después de
hacer una serie de testeos, (en jerga de informáticos “Bootea”) este
arranca, a su vez el sistema operativo (por ejemplo, el Windows o el
Linux).
Es un tipo de memoria lenta pero muy útil, ya que los datos se
guardan y se conservan aún estando apagada la computadora. Suele ser
utilizada en circuito electrónicos que no necesiten mucha energía. CMOS
viene de Complementary Meta Oxide Semiconductor. Para lo cual las
computadoras disponen de una pila recargable para alimentar esta
memoria. Esta pila se recarga cuando la computadora está encendida. Este
tipo de memoria, de la cual hay varias tecnologías diferentes, suelen
ser en la actualidad variantes de la memoria Flash, que es la tecnología
usada en los pen drives.
Sirve fundamentalmente para guardar las configuraciones de la
computadora. Por ejemplo, si yo apago la computadora y le agrego más
memoria, al encenderla el BIOS es el encargado de encontrar cuanta
memoria existe en total sumando el nuevo agregado y este nuevo valor es
guardado en la CMOS. Luego al activarse el sistema operativo (SO), por
ejemplo el Windows, este se entera por el BIOS de la nueva cantidad de
memoria y entonces este SO la puede utilizar, de lo contrario no sabría
de su existencia.
La idea del almacenamiento interno y externo es la de guardar
programas y datos que sobrevivan cuando la computadora esté apagada, o
bien para transportarlos entre computadoras o simplemente para hacer
copias de respaldo (Backups) de datos de mucha importancia. Con la idea
de que estos no se pierdan en caso de fallas con la electrónica o
errores humanos (muy probables!!!).
Hay dos tipos de almacenamiento que se instalan en la parte interna de
las computadoras, el más antiguo, son los discos rígidos. Estos son
dispositivos mecánicos que graban magnéticamente la información sobre
una superficie ferromagnética rotante con geometría de disco.
Típicamente con velocidades de acceso del orden de los
milisegundos.
La otra opción son los Discos de Estado Sólido (o SSD) que si bien se
los llama discos no hay nada circular (ni rotante) en ellos. Son un tipo
de memoria flash que graba en circuitos la información. Tienen
velocidades de acceso en las décimas de milisegundo y se espera que en
un tiempo corto sean tan rápidos como la velocidad de acceso a la
memoria RAM.
A estos dispositivos se los “Formatea”, es decir se construye en ellos
una estructura de índices, para que se pueda guardar y recuperar la
información. Para ser gráfico, pensemos en una biblioteca, el disco es
el cuarto libre. El formateo construye las repisas y los muebles donde
se almacenan los libros y los ficheros que indican su ubicación.
Hay distintos protocolos para formatear un disco, a estos protocolos se
los denomina sistema de archivos (File System,) ejemplos de File Systems
son: FAT32, ext4, etc).
Los periféricos, son todos los distintos dispositivos que se pueden
conectar a la computadora, pueden ser el teclado, el mouse, pantallas,
sistemas de audio, video, etc. Para ello hay distintas interfaces
electrónicas. Las pantallas de Video o monitores suelen conectarse con
enchufes VGA (analógicos), DVI o HDMI (digitales).
El HDMI es un sistema de conexión diseñado para los sistemas de DVD o
Blu-Ray, por lo cual la mayoría de los televisores puede conectarse con
esa interface como monitor de una computadora. Aunque se pueden
conseguir convertidores de HDMI a VGA y viceversa, los sistemas de
conexión digitales son los que proveen una mejor imagen.
Para todos los demás periféricos, los conectores digitales modernos, son
puertos serie (no paralelos), es decir los bits binarios van uno detrás
del otro como una fila de personas. El más utilizado es USB (Universal
Serial Bus), que también es el enchufe típico de los cargadores de
celulares. Actualmente el enchufe tipo A es el más usado, pero se está
reemplazando progresivamente por el tipo C, que es más pequeño y puede
ser usado sin tener en cuenta de que lado se lo conecta, es reversible.
Mientras que el enchufe tipo A, que es el más común, no es reversible.
Vea la Fig. 1.4

Hay sistemas para conectar periféricos que no usan cables, el preferido para dispositivos cercanos es el bluetooth. Normalmente es usado para conectar parlantes, teclados, mouses2 (o ratones en español) y que se utiliza en la mayoría de los celulares. En cambio, las conexiones Wi-Fi son usadas para conexiones a la red internet, aunque bajo ese nombre existe una gran cantidad e incluso diversos protocolos de conexión. También es posible conectar un celular a internet a través de las compañías telefónicas, usando protocolos conocidos como 3G, 4G y en un par de años 5G. Este último es extremadamente rápido y su despliegue cambiará mucho la forma de uso del celular. Para conexiones a corta distancia también existe el bluetooth que es muy usado en el sistemas de audio, desde auriculares para celular a parlantes portátiles.
El Software son las órdenes que se le dan al Hardware para su
ejecución. El software que más usamos es el Sistema Operativo (SO). Este
se encarga del manejo del sistema y de ser la interface entre el usuario
y la computadora. Además se encarga de coordinar los periféricos
(printer, parlantes, etc). Por ejemplo, en una PC es el Windows, en una
computadora de Apple es el MacOSX, o puede ser el Linux. Este último es
un SO gratuito realizado por voluntarios de todo el planeta y es el
sistema operativo más utilizado en muchas áreas científicas.
Cuando uno conecta un dispositivo nuevo a su computadora, este suele
venir con un “driver” o manejador, que le permite al SO “hablar” este
periférico. Estos drivers solían venir en discos pero actualmente los SO
los bajan de internet al momento de localizar que existe un nuevo
hardware conectado a la computadora.
El LINUX es una versión de UNIX y es el que usamos en la cátedra. Los
sistemas UNIX son los que prefieren las personas que usan computadoras
en forma profesional y que programan sus propios códigos. Esto es debido
a que el SO opera mucho más rápido. Por esta razón, estos SO son los
preferidos en los ambientes científicos. Mientras que el Windows o el
MacOSX están pensados para usuarios menos calificados con la idea de
vender estas computadoras como un electrodoméstico mas. A pesar de esto,
el MacOSX tiene un UNIX interno escondido. Las nuevas versiones de
Windows evolucionan a también convertirse en un UNIX, ya que es posible
desde el propio "store" del sistema instalar un sistema que permite
correr órdenes linux de la distribución Ubuntu3. En
ambos casos la idea general es que el usuario no profesional lo utilice
a partir de un sistema gráfico más simple, pero que el usuario más
capacitado y con usos profesionales tenga acceso a un sistema más
complejo en la calidad y variedad de órdenes que se le pueden dar a la
computadora.
Otro ejemplo, son los celulares y tabletas donde existen dos SO que
dominan el mercado en este momento (hay otros con menor cantidad de
usuarios), el Android realizado por Google a partir de portar el Linux a
los celulares y el IOS que se usa en el Iphone. Un punto que hay que
destacar es el interés de los fabricantes de celulares para que en un
futuro cercano haya un SO común entre PCs y teléfonos, con la idea de
que fabriquen computadoras con la tecnología de los celular. Un ejemplo
de esto es la tecnología de la nueva CPU llamada M1 de Apple o los
procesadores ARM que pueden correr Windows.
También hay sistemas operativos conocidos como ‘firmware’’ estos se
usan en dispositivos de uso doméstico y aunque son invisibles al usuario
existen. Se utilizan desde los televisores hasta en los termostatos de
estufas, etc. Si son dispositivos que se conectan a internet,
normalmente su dueño los descubre cuando el aparato pide permiso para
instalar una actualización.
Para darle las órdenes a la computadora hay que usar un lenguaje de
programación. Hay muchos lenguajes y muy diferentes, construidos con la
idea de realizar un tipo de tarea específica. En nuestro caso, el
interés como científicos es el de calcular, analizar y visualizar
datos.
En esta cursada la idea es que los alumnos dominen dos lenguajes: el
Fortran que es muy antiguo pero útil para hacer programas de cálculo muy
pesados y el Python que es uno de los lenguajes más usados en el
análisis de datos. En el caso del Python, este es un lenguaje moderno y
orientado a objetos (más adelante veremos qué es un objeto) a diferencia
del Fortran. Pero con una desventaja al ser tan actual: continuamente se
lo mejora pero sin mantener la compatibilidad con versiones anteriores,
lo que obliga a revisar programas de hace unos años o meses.
En general hay dos clases de lenguajes para programar una computadora,
los que son compilados o los que son
interpretados. El lenguaje Fortran es compilado, es
decir se escriben las órdenes y este conjunto de órdenes (todas juntas)
son convertidas (o traducidas) a un programa ejecutable que es el que
entiende la CPU de la computadora.
Por lo tanto en Fortran tengo 3 etapas: programar el código, compilarlo
y luego puedo correr el ejecutable que es el resultado de esta
compilación.
En el caso de los interpretados (como el Python), cada orden (o un
conjunto de estas) del programa es convertida a órdenes del CPU y luego
ejecutada, para pasar a la orden que sigue, esto permite trabajar con
más interacción con el código, pero los programas son más lentos porque
el método es poco eficiente. Pero por otro lado es más fácil encontrar
errores en el código o realizar mejoras en el momento, y en computadoras
muy rápidas la ineficiencia del interprete pasa mucho más
desapercibida.
En lenguajes interpretados modernos a veces estos se usan como un frente
(frontend) para llamar a códigos ya compilados (backend) y estamos en un
caso híbrido entre compilados e interpretados. Por ejemplo, esto se
utiliza con los sistemas de Machine Learning.
En el caso del Fortran este tiene una cantidad no muy grande de
órdenes a disposición del usuario pero estas son suficientes para
realizar todas las operaciones que se pueden encontrar en un libro de
álgebra. En el caso del Fortran no se le están agregando nuevos
comandos. Mientras que el lenguaje Python tiene un filosofía de trabajo
diferente en la cual se pueden agregar órdenes y funciones construidas
por otros autores como si fuesen nativas del sistema, por lo cual la
cantidad de comandos es inmenso en número, variado en temas y a su vez
evoluciona rápidamente con el tiempo. Veremos con detalle estas
diferencias durante la cursada.
Existen varios tipos de Variables Numéricas utilizadas en los
sistemas digitales, pero antes de prestar atención a sus características
es necesario discutir un punto que es importante al usar computadoras.
Estas difieren en como se representan internamente los números con
respecto a cómo lo hacemos nosotros los humanos. Esto es debido a que
las computadoras trabajan en base binaria (base 2) y no en base decimal
(base 10).
¿Cómo es esto?
Las computadoras utilizan señales eléctricas para transportar, procesar
y guardar la información. Es decir, tienen cables metálicos que llevan
pulsos de corriente eléctrica. El pulso o la falta de este en el momento
adecuado es usado como información. Entonces, si hay un pulso eléctrico
en un cable lo anotamos con un 1 y si no lo hay con un 0. Como sólo
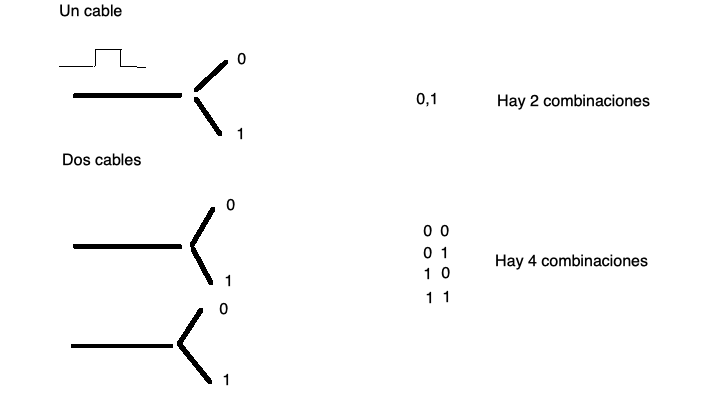
están estas dos posibilidades hablamos de un sistema binario. Supongamos
que tenemos un sólo cable, bueno sólo puedo tener dos números el 0 y el
1, esta configuración se la llama bit (ver fig. 2.1). Un sólo cable no es muy útil, sólo
tenemos un sistema que puede representar dos números. La forma de
resolver esta situación es la de agregar más cables. Veamos entonces que
sucede si agregamos un cable más. Con dos cables tendremos 0,0 (ambos
cables sin un pulso eléctrico), 0,1 y 1,0 (si uno tiene el pulso y el
otro no) o 1,1 (en el caso que los dos cables lleven un pulso
eléctrico). Es decir, con dos cables se obtienen 4 configuraciones
diferentes que me permiten representar 4 números. Es obvio entonces que
agregando más cables puedo representar más números. La tabla 2.1 describe lo que va pasando a
medida que agregamos más cables.
| Cantidad de Cables | Cantidad de números | Potencia de 2 ( \(2^n\)) |
| N (bits) | que puedo escribir | |
| 1 | 2 | 1 bit \(\rightarrow\) \(2^1=2\) |
| 2 | 4 | 2 bits \(\rightarrow\) \(2^2=4\) |
| 3 | 8 | 3 bits \(\rightarrow\) \(2^3=8\) |
| 4 | 16 | 4 bits \(\rightarrow\)\(2^4 =16\) |
| ... | ... | ... |
| 8 | 256 | 8 bits \(\rightarrow\)\(2^8=256\) \(\leftarrow\) Byte |
| ... | ... | ... |
| 10 | 1024 | 10 bits \(\rightarrow\)\(2^{10}=1024\) \(\leftarrow\) Kilobits [Kb] |
| ... | ... | ... |
| 20 | 1048576 | 20 bits \(\rightarrow\)\(2^{20}=1048576\) \(\leftarrow\) Megabits [Mb] |
| ... | ... | ... |
| N | M | N bits \(\rightarrow\)\(2^N=M\) |
| Símbolo | Prefijo | MKS | Binario | Diferencia Porcentual | Ref |
|---|---|---|---|---|---|
| K | kilo | \(10^3 = 1000^1\) | \(2^{10} = 1024^1\) | 2.40% | |
| M | mega | \(10^6 = 1000^2\) | \(2^{20} = 1024^2\) | 4.86% | Memoria Cache |
| G | giga | \(10^9 = 1000^3\) | \(2^{30} = 1024^3\) | 7.37% | Memoria RAM/SSD |
| T | tera | \(10^{12} = 1000^4\) | \(2^{40} = 1024^4\) | 9.95 % | Discos Rígidos/SSD |
| P | peta | \(10^{15} = 1000^5\) | \(2^{50} = 1024^5\) | 12.59% | Grandes Servers |
| E | exa | \(10^{18} = 1000^6\) | \(2^{60} = 1024^6\) | 15.29% | Datacenters/Nube |
| Z | zetta | \(10^{21} = 1000^7\) | \(2^{70} = 1024^7\) | 18.06% | |
| Y | yotta | \(10^{24} = 1000^8\) | \(2^{80} = 1024^8\) | 20.89% |
En la tabla 2.1 se puede ver la definición de
Byte (B en mayúscula) frente a la de bit (b en minúscula). Recordar que
un Byte son 8 bits, por ejemplo: 1110001 o 00011111.
El Byte es la unidad de memoria de información en las computadoras.
Ejemplos: la memoria se mide en Gigabytes (mil millones de Bytes), los
discos rígidos en Terabytes (millón de millones de Bytes). Por ejemplo,
la velocidad de conexión a internet puede ser medida en unidades de
bit/segundo o Bytes/segundo. Pregunta inquietante para resolver: ¿Qué
velocidad tienen en la conexión a internet en sus hogares? ¿Cuánto en
Bytes y cuánto en bits? ¿Es simétrica? Es decir ¿La bajada de
información de la red tiene una velocidad igual a la subida?
También hay que notar que se usan unidades parecidas al MKS, pero
no son iguales en tamaño, un kilo MKS es \(1000=10^3\) pero un Kilobyte es \(1024=2^{10}\). No es la misma relación. Lo
mismo para un megabyte \(1048576 =
2^{20}\) que no es \(10^6\) como
son las unidades MKS. La tabla 2.2 nos
muestra como las notaciones binarias y decimales difieren cuando los
números se vuelven más grandes, aunque los nombres que se usan en los
dos sistemas de unidades son los mismos. Esta situación es causante de
muchas confusiones.
En un intento de resolver la falta de claridad de estas unidades, la
Comisión Electrotécnica Internacional (IEC) en diciembre de 1998
estableció el estándar de almacenamiento de 1024 bytes con la
nomenclatura de KiB en vez de kB como era anteriormente y denominarlo
kibibyte, para diferenciarlo del kilobyte. Por lo cual, 1 kibibyte =
1024 B = \(2^{10}\) bytes y 1 kilobyte
= 1000 B = \(10^3\) bytes. Si bien esta
comisión establece los estándares internacionales, lo que terminó
creando fue una mayor confusión, ya que esta unidad nueva es muy poco
usada e incluso grandes empresas la ignoraron por completo (por ejemplo:
Microsoft, Apple la usa en forma parcial, etc). Tampoco en el área de la
astronomía o en la ciencia en general esta nueva unidad ha tenido algún
éxito y esta forma de notación no es usada.
Cuando uno habla de base numérica se refiere a que si uso base 10, es 10
justamente el primer número que tengo que componer utilizando caracteres
ya existentes (en este caso el 1 y 0). En binario, que es base 2, es
entonces el número “2” el que se escribe como 10 en esa base. El número
45 en base 10 se sobreentiende que es \(4 x
10^1 + 5 x 10^0 = 45\) (note como la base es la que caracteriza
el orden de magnitud de los dígitos), pero en binario este número sería:
101101, ya que \(1 x 2^5 + 0 x 2^4 + 1 x 2^3 +
1 x 2^2 + 0 x 2^1 +1 x 2^0 = 32 + 8 + 4 + 1 = 45\)
Otra de base que se usa mucho en computación, tecnologías
electrónicas y digitales es la base 16 o hexadecimal. Por lo que
explicamos antes, en esta base el 16 se escribe como el número 10. En la
tabla 2.3 hacemos la conversión entre
diferentes bases para los primeros 16 números naturales.
| Número Decimal | Binario | Hexadecimal |
| Base 10 | Base 2 | Base 16 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Por convención, los números hexadecimales se los escribe con un “0x” delante para indicar la base 16. Por ejemplo, 0x9AD3 o 0x45FC ¿Cuál sería entonces, la ventaja de usar número en una base tan “antinatural” (por decirlo de alguna manera) como es la base 16? Hay una razón simple y es la siguiente: 4 bits (o sea medio Byte) describe todos los números posibles entre 0 y 15 (ver la tabla 2.1) entonces 1 Byte puede ser escrito como dos números hexadecimales. Por ejemplo, el numero binario 10011111 se podría escribir como 0x9F (1001 \(\rightarrow\) 9 y 1111 \(\rightarrow\) F) y esto evita un problema importante que tienen los números binarios, ya crecen muy rápidamente en la cantidad de dígitos cuando los números son grandes y por lo tanto se vuelven complicados de escribir, recordar, etc y en general, de manejar. Con los hexadecimales sucede la situación inversa, para un mismo número su escritura es más corta en cantidad de dígitos que su versión decimal y todavía mucho más corta que la representación binaria, con la ventaja de la correspondencia directa que tienen con los números binarios.
El Byte es la definición de la unidad de memoria y proceso de una computadora, por lo tanto sólo, se puede utilizar una cantidad entera de Bytes en cualquier proceso digital. No existen ni se usan las fracciones de Bytes. Es básicamente el ladrillo con que se construyen las unidades de información (más delante esta idea quedará más clara) en los sistemas digitales.
En los sistemas de computación, la forma de manejar los distintos tipos de números (enteros, reales, etc.) dependen de una combinación de Hardware y Software. Mientras las operaciones matemáticas básicas la realiza el Hardware en la CPU, la definición completa de las atribuciones de los números depende del Software a usar. Dicho de otra manera, cada lenguaje de computación tiene algunas definiciones diferentes de las propiedades de los números que usa. Veremos en este curso cómo los números binarios se usan para construir los distintos tipos de variables numéricas en los Lenguajes FORTRAN y PYTHON.
Con los Bytes que vimos en la sección anterior se construyen los número que usamos en nuestros cálculos. Así como se ve en un curso de Análisis Matemático hay diferentes clases de números, por ejemplo, naturales, enteros, reales, complejos, etc, lo mismo pasa en los sistemas de computación. Veamos los tipos más comunes de construcciones numéricas y luego estudiaremos cómo se usan en cada lenguaje.
Los enteros (integer en inglés) utilizan típicamente de 4 u 8 Bytes
para su construcción, aunque muchos sistemas pueden usar a pedido del
usuario 2 Bytes o una cantidad mayor de Bytes (16 o más)
¿Cómo se usan estos bytes?
Cada Byte tiene 8 bits, y con estos se construyen en base binaria los
números. Estos pueden tener o no tener signo (unsigned en inglés) y
serían solo los números positivos (naturales) o con signo (signed), que
serían los números enteros tal cual se definen en un curso de
matemática. Si el número es unsigned y tengo 4 Bytes (32 bits) podría
escribirse \(2^{32}-1\) números, en si
todos los números del intervalo [0, 4294967296]. En cambio, si es signed
tendré que usar uno de los bits para indicar si el número es positivo o
negativo, quedándome con 31 bits para escribirlo. Con estos 31 bits
puedo construir \(2^{31}\), pero cómo
tengo positivos y negativos me quedan los números entre [-2147483648,
2147483647].
Como ya aclaramos, se pueden usar más o menos Bytes para representar el
número entero. En la tabla 2.4 vemos
para diferentes usos de los Bytes y los intervalos de números que
logramos representar.
| Bytes | bits | Sin signo (unsigned) | Con signo (signed) |
| n | \(8 n\) | max. número (\(2^{8n}-1\)) | intervalo de números |
| 1 | 8 | 256 | [-128, 127] |
| 2 | 16 | 65535 | [-32768, 32767] |
| 4 | 32 | 4294967295 | [-2147483648, 2147483647] |
| 8 | 64 | 18446744073709551615 | [-9223372036854775808, 9223372036854775807] |
Las operaciones con números enteros se realizan en una unidad especifica para tal fin en la CPU. Eso significa que las operaciones básicas (suma, resta, multiplicación, división, etc) se realizan en esa unidad que es sólo para cálculos con números enteros. Hay que tener en cuenta que la división de enteros sólo puede dar como resultado otro número entero, perdiéndose la parte fraccionaria del número resultante de esta operación. Ejemplo, 7/3 da como resultado 7/3=2
Los números reales son más complicados en muchos sentidos, ya que se escriben internamente en la computadora en binario en forma de una mantisa y un exponente. Estos números se los llama flotantes debido a que el problema original de los ingenieros era que el punto decimal flotaba y podría estar en cualquier lugar del número. Pero en sí, esa no es la dificultad más importante, sino que los números reales pueden tener infinitos decimales y no existe tal cosa como memoria infinita en una computadora. En algunos casos los números reales deben ser cortados (o truncados), perdiendo los últimos dígitos de la parte fraccionaria, ya que no se pueden guardar. Veremos más adelante que esta pérdida de decimales trae consecuencias (malas!) en algunos cálculos donde la propagación de errores es importante, pero también que existen formas para disminuir el efecto de este problema. Estos flotantes se representan utilizando una cierta cantidad de bits (de los Bytes) distribuyéndolos en el signo del número, la mantisa y el exponente.
Básicamente, un número sería en binario: \(\pm mantisa\ x \ 2^{\pm exponente}\). La norma IEEE-754 utiliza 4 Bytes (32 bits) para los reales simples, donde 8 bits son para el exponente y los 24 restantes para la mantisa y el signo.
A veces en cálculos muy precisos esta representación de los números no alcanza, ya que se necesita una mayor cantidad de decimales significativos de los que usando. En esos casos se pueden usar reales de 8 Bytes (se los denomina como real*8 o doble precisión) con lo cual hay 64 bits para repartir entre mantisa y exponente. Las operaciones que se realizan con números real*8 conservan más decimales significativos. En algunos lenguajes de programación permiten definir real*16 (o sea 16 Bytes para escribir el número), pero estas variables no son las más comunes, ya que se necesita que el hardware pueda manejarlas. Definir números como real*8 o real*16 puede acarrear dos problemas: el primero es que se necesita más memoria para guardarlos y por lo tanto tiempo en esta tarea, y en el caso de real*16 mayor tiempo de cálculo. Las operaciones con números reales se realiza en las unidades de punto flotante de la CPU que es un circuito electrónico diferente del que realiza las operaciones con enteros. En el caso de real*8 se utilizarían entonces 64 bits, tomados de la siguiente forma: 1 bit para el signo, 11 para el exponente, y 52 para la mantisa. Esto significa que los valores que podemos representar van desde \(\pm2.2250738585072020 x10^{ -308}\) hasta \(\pm1.7976931348623157×10^{308}\).
En base a lo que vimos antes es importante señalar que si escribo 1.0 o 1. (sin poner el 0) este número es real, mientras que el 1 (sin el punto decimal) es un número entero. Las dos formas de representar el número como real o como entero no tienen la misma representación binaria dentro de la computadora.
Los números complejos se los considera como números con dos componentes reales y cada lenguaje tiene sus protocolos propios para describirlos. Las operaciones con números complejos están implementadas correctamente en los lenguajes que los soportan. Es decir, el sistema realiza operaciones sabiendo que \(i^2=-1\).
Si bien las computadoras realizan todas sus operaciones en binario,
los resultados son convertidos a notación científica al mostrarlos al
usuario cuando la situación lo requiera. Un caso de interés es como
muestran la notación científica ya que lo hacen indicando con la letra
E que lo que sigue del número es el exponente en base
10.
Ejemplos:
1E23 es el número \(1\ x\
10^{23}\)
4.345E03 es el número \(4.34\ x \
10^{3}\) o sea el 4340
También existe la posibilitad de que el exponente sea negativo así que
el número 24323E-45 es el \(24323\ x\
10^{-45}\) En Fortran, también se puede en vez de la E usar la
letra D, indicando que el número debe ser considerado tanto para
guardarse en memoria o en las operaciones matemáticas como doble
precisión (real*8).
r0.50 
El nombre Fortran viene del inglés “The IBM Mathematical
Formula Translating System”, es decir
sistema traductor de fórmulas de IBM. Con el tiempo acortaron el nombre
a FORTRAN. Es un lenguaje de alto nivel4
diseñado para ser utilizado en los ambientes científicos, básicamente de
cálculo. Las primeras versiones del lenguaje son del año 1957 y de ahí
en adelante ha evolucionado siendo la base de muchos lenguajes modernos.
Puede manejar variables, incluyendo vectores y matrices. Tiene muchas
décadas de uso, testeo y optimización, por lo cual es muy eficiente ya
que sobrellevó muchas correcciones que lo mejoraron durante un largo
período de tiempo (más de cuatro décadas).
Tiene puntos a favor y también puntos en contra. Si resumimos, estos
son:
A favor:
Mucha experiencia y compiladores extremadamente eficientes. Son muy rápidos y con resultados finales excelentes.
Es un lenguaje simple, muy rápido de aprender. Pocas órdenes y concisas frente a lenguajes más modernos.
Compatible en sus estructuras con otros lenguajes (C o Python).
Los compiladores pueden optimizar el código para el hardware existente.
Existen Infinidad de algoritmos ya programados, que se pueden encontrar en libros o en internet.
Se puede escribir en mayúscula o minúscula indistintamente.
Se aprende rápido, y el código escrito de un programa es fácil de leer.
En contra:
Alguna de la sintaxis de las ordenes provienen de la época que se perforaban tarjetas.
No es orientado a objetos.
En los lenguajes modernos hay muchas más funciones y algoritmos pre-programados (bibliotecas).
No incluye un sistema para hacer dibujos o gráficos.
No es interactivo y no tiene mucha utilidad fuera de los requerimientos de científicos o de ingeniería.
Aunque parece que hay otras consideraciones sobre el Fortran fuera de este planeta (ver figura [fig:qr_simpsons]).
Si doy en Fortran la siguiente orden:
I=5
IMA=23
FE4=484.22
r0.30 
Estoy guardando el número que está a la derecha del signo “=” en el nombre (imagínense que es una caja) que está a la izquierda. Es decir en la variable que se llama “I” guardo dentro de ella el número 5 (un número entero), en la que se llama IMA guardo un 23 (entero). Pero en la que se llama FE4 guardo un número real el 484.22.
Esta operación se conoce con el nombre de asignación y en este caso el símbolo de “=” causa la asignación, pero este “=” no es para indicar una igualdad, es decir, no es el “igual” que acostumbramos ver en una ecuación, aunque como veremos más adelante se le parece mucho. Los nombres de la variables siempre deben empezar con una letra, pero después de esa letra pueden tener números. Otros lenguajes (ni Fortran, ni Python) para evitar la confusión entre ecuaciones y asignaciones han usado otro símbolo para la operación de asignación, pero en la mayoría se usa el “=”.
Hay que prestar atención que las computadoras (al igual que las calculadoras de mano) utilizan la nomenclatura anglosajona para los puntos y las comas, es decir las usan al revés que en español. La coma que usamos para indicar la parte fraccionaria del número es ahora un punto. Es decir, el número 23,5 (23 y medio) es ahora 23.5 (con punto en vez de coma).
Hay 5 tipos de variables en Fortran distintas y con propiedades
únicas. Tres de estos tipos guardan números. Estas son:
Enteras (Integer)
Reales (Float)
Complejas (Complex)
Lógicas (Logical/Boolean)
Texto (Character)
Veamos cada una de ellas:
Las variables Enteras en Fortran, pueden ser de 2, 4 u 8 Bytes, y se definen usando la sentencia (u orden) Integer*n donde n es la cantidad de Bytes que voy usar en ese número en particular. Con más Bytes se pueden escribir números con mayor cantidad de dígitos tanto negativos como positivos). Si el nombre de la variable empieza con alguna de estas letras I,J,K,L,M o N la variable será entera por definición (default)5, a menos que se de una orden en contrario. Las variables enteras son muy útiles para manejar los subíndices en un matriz o en un vector, por ejemplo.
Si escribo:
INTEGER cuenta
La variable cuenta, ahora sólo sirve para cargar
números enteros, no podría albergar a un número real. Por ejemplo, si
ahora ordeno la siguiente operación:
cuenta = 3.141549
En cuenta solo se habrá guardado un 3 y los decimales se perdieron. Ya
que cuenta es un número entero y estos no pueden guardar decimales.
Las variables reales en Fortran son de 4 Bytes (
REAL*4) o 8 Bytes ( REAL*8 o también
conocidas como doble precisión). Cualquier variable con un nombre que
comience con las letras de A hasta la H y desde la O hasta la Z, es por
definición REAL*4. Si quiero que sea
REAL*8 tengo que indicarlo con un orden específica que
será:
REAL*8 Mag, Mag1, Mag2
Habiendo dado esta orden las variables Mag, Mag1, Mag2 ahora sólo
guardan números reales de 8 Bytes, mientras que si no hubiese dado esa
orden serían variables enteras porque sus nombres comienzan con M.
Existe la orden DOUBLE PRECISION y es equivalente en todo a poner REAL*8.
En casos muy extremos puede usarse la orden REAL*16 (precisión cuádruple) donde la representación binaria el número será mucho más extensa (128 bits) permitiendo una menor pérdida de precisión en la operaciones, pero en la mayoría de las computadoras no es soportada por el hardware, y por lo tanto es una orden que se ejecuta corriendo software, por lo cual no sólo es importante el consumo de memoria ram (4 veces más que un REAL*4) sino que el tiempo de cálculo se vuelve mucho más largo. Dicho de otra manera, utilizar variables REAL*16 implica entender que se usarán muchos más recursos en la computadora tanto en tiempo como en memoria y sólo debe utilizarse en casos que lo justifiquen.
Las variables complejas utilizan dos números, uno para la parte real
y otro para la parte imaginaria. Los números complejos pueden ser real*4
o real*8, y definido un número como complejo ambas parte real e
imaginaria son del mismo tipo. Los complejos en Fortran se representan
como un par ordenado (a,b), en donde a es la parte real y b la
imaginaria. (a,b) es el número \(a\ +\ b\
i\).
Para construir una variable para que guarde números complejos tengo que
usar la orden complex. Ejemplo:
COMPLEX A1,A2,A3,A4
De aquí en adelante las variables A1,A2,A3 y A4 sólo guardarán números
complejos.
Las variables lógicas o Booleanas, solo pueden contener un Verdadero
(en inglés:True) o Falso (False). Para ellos usan un Byte, en el que
sólo activan o no uno de bits (si, desperdiciando 7 bits). En Fortran,
el Verdadero se escribe como .true. y el false como
.false.. Note que ambas palabras tienen
puntos adelante y atrás. Estos puntos se ponen para
diferenciar un verdadero o falso de una variable o texto que se llamara
“true” o “false”.
Para que una variable sea Booleana tengo que usar la orden
Logical. Ejemplo:
LOGICAL L1,L2,L3
Ahora las variables L1, L2 y L3 sólo guardarán Verdaderos o Falsos.
Las variables de caracteres, utilizan 1 Byte por cada letra que yo
quiera representar. Por ejemplo si quiero guardar un texto de 25
caracteres, tendría que definir la variable para esta cantidad de
caracteres o más (me pueden sobrar, aunque eso agregaría espacios en
blanco). Lo haría de esta manera:
CHARACTER*25 cartel
Entonces la variable cartel guarda un texto de hasta de 25 caracteres.
La idea de que un Byte es un caracter viene de la definición de códigos
ASCII que veremos más adelante, en ella cada letra tiene un número
binario de un byte definido por convención para todos los fabricantes de
computadoras, esa definición fue modificada para albergar mas caracteres
en los que se llama UNICODE donde se llegan a usar hasta 4 Bytes.
En Fortran hay una manera de convertir cualquiera de los tipos de
variables que vimos antes, en un vector, matriz, cubos y estructuras con
más dimensiones. La orden más antigua para esta tarea es la DIMENSION, y
se usa así:
DIMENSION A(10)
Esta orden que se pone al principio del programa, define que la variable
A, tiene 10 componentes y que estas serían: A(1),A(2),A(3),...,A(9) y
A(10). Cada una de estas componentes actúa ahora como una variable que
puede guardar números. Si escribiera la siguiente sentencia:
DIMENSION B(100,100)
Ahora B es una matriz de 100x100 elementos, y por ejemplo existe como
variable B(22,97)
La forma más moderna de usar esta orden es así:
REAL*8 B(100,100), C(100,100,100)
donde aprovecho y fijo el tipo de variable y su dimensión.
Las variables que comiencen su nombre con una letra determinada son
reales (real*4) o enteras. Si no me sirve esa definición, la puedo
forzar con un comando. Por ejemplo, en astronomía medimos los flujos de
energía que emite una estrella como su magnitud. Magnitud empieza com M
entonces la palabra sólo guardaría un número entero, pero eso no nos
sirve, las magnitudes son números reales, entonces, defino:
real*4 magnitud
Ahora con esta nueva definición me sirve para guardar números
reales.
Puedo re-definir de una sola vez y en una sentencia, muchas variables
variables:
real*8 ixag, jxag1, kxag2, lxag4
integer xa, xb, xf5, ser
complex*8 a, b, c
complex*8 x(100) \(\ \ \ \ \
\ \ \) \(\rightarrow\) X es
ahora un vector de números complejos y doble precisión de 100
elementos
En Fortran 90/95 se cambió la forma de definir las variables. En este
nuevo sistema se separan con “::" (dos :) la parte del tipo de variable,
de una lista de nombres de variables que se definirán de ese tipo
específico.
Tipo específico:: Lista de VariablesVeamos unos ejemplos:
Las variables ZIP, Media and Total quiero que sean del tipo INTEGER
INTEGER :: ZIP, Media, TotalLas variables promedio, error, sum and ZAP quiero que sean del tipo REAL
REAL::promedio, error, sum, ZAPY las de tipo CHARACTER
CHARACTER(LEN=15) :: Name, StreetLEN=15 significa que se usan 15 lugares (Bytes) para las letras
Como hemos contado, las órdenes en Fortran se escriben como una serie
de renglones como un texto. Cada uno de estos renglones es una orden (o
sentencia) que se ejecutará una detrás de la otra en orden. El primer
renglón es la primera orden, luego de esa se ejecuta la sentencia del
segundo renglón y así sucesivamente hasta la último (aunque existen
órdenes que permiten volver a pasar por las mismas sentencias una y otra
vez que estudiaremos en los siguientes capítulos).
Ya hemos adelantado lo que es una asignación en la sección anterior a
esta, es decir, cómo cargar una constante en una variable del programa.
Por ejemplo:
I=5
donde a la variable entera I le asignamos el número 5.
En Fortran se utilizan las operaciones básicas con los símbolos que utilizamos comúnmente (+, -, /), salvo por el signo de multiplicación donde no usa la “x” sino que se usa el símbolo “*”, que de hecho muchos teclados de computadora ya la tienen marcada así, en la zona derecha en la parte del teclado numérico. Otra operación básica que tiene una notación distinta es la potencia. No podemos poner \(x^2\) porque no puedo escribir en mitad de los renglones de una computadora (no hay supraíndices, tampoco subíndices). Por eso la potencia se escribe como dos asteriscos seguidos. Es decir, \(x^2\) se escribe como \(x**2\)
Las prioridades de las operaciones básicas son las mismas que las que
se establecen en el álgebra.
Por ejemplo, puedo escribir:
A = b1 + c4 / x
Esta orden dividiría el valor guardado en c4 por x y el resultado de ese
valor se lo sumaría a b1. El resultado final de toda la operación se
guardaría en A. Note que las multiplicaciones y divisiones tienen
prioridad sobre las sumas y restas. Pero puedo usar los paréntesis
adecuados para acomodar el cálculo a mi gusto. Por ejemplo:
A = (b1 + c4) / x
Ahora las operaciones se hacen en diferente orden, por la posición de
los paréntesis se sumarían b1 más c4 y recién el resultado se dividiría
por x.
Las asignaciones no son ecuaciones, y veamos por qué. ¿Cómo haría si
quisiera saber en un cierto código cuántas veces este programa pasa por
un determinado lugar, para volver a realizar el mismo cálculo? La idea
sería tomar una variable para usar como contador, y sumarle un uno cada
vez que paso por el lugar donde se encuentra. Es decir con una sentencia
como esta:
I = I + 1
En esta sentencia se busca el valor de I que se encuentra en la memoria,
se le suma un uno y se lo vuelve a guardar en la variable I. Como vemos
esto no es una ecuación, es un procedimiento de derecha a izquierda
donde se guarda el resultado. Por eso las asignaciones no son ecuaciones
pero se les parecen, nada evita que yo escriba:
E = M * C**2
En donde hago el cálculo de energía de la famosa ecuación de Einstein
\(E = MC^2\). Pero no hay que
confundirse, una es una ecuación de la física y la otra es la sentencia
para hacer el cálculo en Fortran.
El lenguaje Fortran tiene una serie muy importante de funciones matemáticas preprogramadas, estas incluyen trigonometría, raíz cuadrada, logaritmos, exponencial, etc. Muchas de estas funciones se calculan usando el hardware, es decir, hay circuitos en la CPU que las pueden calcular a velocidades muy altas. En la tabla 4.1 veremos algunas de las más usadas.
| Función | Nombre en Fortran | Función | Nombre en Fortran |
|---|---|---|---|
| \(sen(x)\) | SIN(X) | \(cos(x)\) | COS(X) |
| \(tan(x)\) | TAN(X) | \(arcsen(x)\) | ASIN(X) |
| \(arccos(x)\) | ACOS(X) | \(arctan(x)\) | ATAN(X) |
| \(\acute{a}ngulo(y,x)\) | ATAN2(Y,X)\(^*\) | \(\mid x \mid\) | ABS(X) |
| \(\sqrt{x}\) | SQRT(X) | \(e^{(x)}\) | EXP(X) |
| \(\ln(x)\) | LOG(X) | \(log(x)\) | LOG10(X) |
Ejemplos:
\(z = \sqrt{(x^2 + y^2)}\)
en Fortran sería: z = sqrt(x**2 +
y**2)
\(x =e^{\frac{1.}{4} y^2}\)
en Fortran sería: x = exp(1/4*y**2)
\(z = \frac{1+\frac{1}{x}}{3x +
2}\)
en Fortran sería: z= (1+1/x)/(3*x+2)
\(\omega = \cos(\alpha + \phi) + \cos \alpha
\cos \phi - sen \ \alpha \ sen \ \phi\)
en Fortran sería: omega = cos(alfa + fi) + cos(alfa) * cos(fi) -
sin(alfa) * sin(fi)
donde al no tener letras griegas, escribo sus nombres, como nombres de
las variables que uso.
Una vez que, por ejemplo, la variable A está definida como un vector
de 10 elementos, podríamos hacer lo siguiente:
REAL*8 A(10)
A(8) =22.543434
I = 5
A(9)= A(8) * A(I)
En este caso, como I toma el valor 5, el A(I), es A(5).
Es decir, los índices de los vectores y matrices pueden también ser
variables, que por razones obvias tienen que ser enteras. Por lo cual,
si se acuerdan de los teoremas del Álgebra sobre matrices, estos siempre
se definen sobre un elemento genérico \(a_{(i,j)}\) y en Fortran sería la variable
A(I,J). Dicho en otras palabras, en Fortran y los demás
lenguajes de computación podemos manejar el mismo nivel de abstracción
que en matemática.
En esta sección analizaremos la estructura básica de un programa
Fortran (que es similar a otros lenguajes). Primero hay que ver las
reglas para escribir los renglones y recordar que cada renglón es una
orden.
Estas son:
En Fortran 77 (y anteriores), las primeras 6 posiciones se reservan y
las órdenes se deben escribir a partir de la columna 7 hasta la columna
72. Si en las primeras columnas aparece una letra C o
un *(muy raro que vean este símbolo para esto), ese
renglón es un comentario sin ninguna orden activa, lo cual es muy bueno
para hacer anotaciones de lo que trata lo que estamos programando, y por
ejemplo, qué significa cada variable o de dónde sacamos el algoritmo,
etc. Siempre es bueno tener muchos comentarios sobre lo que se hace,
para recordar datos útiles de la tarea que se realiza en ese segmento
del programa. A veces se trabaja en un grupo de investigación con otras
personas y buenos comentarios ayudan a una mejor interacción con los
colaboradores. Fortran 90 agregó el símbolo ! como otra
indicación de comentario con la ventaja de que puede ser puesto en el
mismo renglón que una sentencia activa a continuación de esta.
Si tengo una orden muy larga, y ya llegué escribiendo a la columna 72 y necesito más espacio para escribir, lo que tengo que hacer es incluir en la línea de abajo algún caracter en la columna 6 y eso le avisa al compilador que sigue la orden de la línea de arriba. Esto se puede repetir todo lo que sea necesario, es decir, una sentencia podría extenderse por decenas de renglones. Se puede poner números de las columnas 0 a la 6 y esos números indican posiciones determinadas en el programa. Me permitirán hacer que mi programa retome alguna de esas líneas (veremos más adelante cómo hacer esto). Esos números que pueden ser discontinuados (se puede poner 99, sin que existan los 98 anteriores) actúan como si fuesen carteles indicando posición. Son sólo una etiqueta indicando un lugar en el programa.
Resumiendo:
Col. 1 En blanco o “c” o “*” para comentarios
Col. 1-5 : En blanco o uso como etiqueta (opcional)
Col. 6 : Continuación de la línea anterior (opcional)
Col. 7-72 : Sentencias
Col. 73-80: Se pueden usar como comentarios, ya que lo que está acá es
ignorado por el compilador.
Ejemplo de continuación en la línea de que sigue abajo:
c23456789 (Uso este comentario para tener una
referencia del número de columna!)
La siguiente sentencia la escribo en dos renglones:
\(\ \ \ \ \ \ \ \ \ \) area = 3.14159265358979
\(\ \ \ \ \ \ \ \) + * r *
r
Veamos un programa simple, pero completo en el sentido de que tiene
todas las estructuras que se usan en programas mucho más grandes tanto
en largo como en recursos. Para ello vamos a tener una meta, hacer un
código que calcule el área de un triángulo, que es: Área = (Base x
Altura) / 2.
Este sería el programa:
C234567
Program areat
C Programa para realizar el calculo del área de un triángulo rectángulo.
C Ingresando la base y la altura}
real*8 base, altura, area
read(*,*) base, altura
area = (base*altura)/2
write(*,*) 'El area es =',area
endLa idea es ahora analizar sentencia por sentencia lo que este programa hace y que significa frente a la estructura general que se utiliza para programar en Fortran.
\(\ \ \ \ \ \ \ \) Program
areat
Esta orden da nombre al programa, puede tener algún significado especial
en algunos SO o compiladores.
C Programa para realizar el calculo del área de un triángulo
rectángulo.
C Ingresando la base y la altura
Estas dos líneas, empiezan con la letra C así que son comentarios, me
sirven a mí, por ejemplo, para recordar que se está calculando, cuál es
el significado físico de cada variable y cuál es el método del cálculo,
etc. El compilador las ignora y para el resultado final da lo mismo que
estén o no. Pero les recuerdo, es muy bueno comentar lo que se hace en
cada sección de un programa.
\(\ \ \ \ \ \ \ \) real*8 base,
altura, area
En esta orden convertimos las variables base,
altura y area de real*4 que sería la
definición estándar a real*8 que asegura más decimales, aunque hay que
comentar que en este caso particular esto no tendría mucho sentido a
menos que se justifique la necesidad de una mayor precisión en los
cálculos. Esto es lo que se debe hacer al comienzo de los programas en
Fortran (y en muchos otros lenguajes) tenemos que definir al comienzo la
forma y el tipo de las variables que vamos a usar. Puede que en programa
muy importante existan cientos de líneas definiendo variables.
\(\ \ \ \ \ \ \ \) read(*,*)
base, altura
En esta sentencia hacemos una entrada de datos al
programa, eso lo hace la orden read (leer en inglés).
Esta orden tiene un paréntesis en el cual hay dos “*” . El primer “*” es
de dónde yo leo, si está el “*” significa que el programa lee los
números del teclado donde corre el programa. El segundo “*” es cómo los
leo, ahí podría indicar por ejemplo la cantidad de decimales, etc. Si
hay un “*” dejo que la computadora decida. Los asteriscos funcionan como
una especie de definición estándar delegando en la computadora la toma
de decisiones, en la mayoría de los casos puede ser una buena idea, pero
no siempre. Luego en la orden están las dos variables a leer, por lo
cual el programa detiene su ejecución y espera que escribamos en el
teclado los valores. Primero uno y luego el otro separado por un blanco
(también se podría haber puesto una coma separándolos).
\(\ \ \ \ \ \ \ \) area =
(base*altura)/2
En esta sentencia hacemos el cálculo y asignamos el resultado a la
variable area. Esta sería la zona de cálculo del
programa, en otro programa ser el área de cálculo podría muy extensa y
contar con miles de líneas.
\(\ \ \ \ \ \ \ \) write(*,*)
´El area es =´,area
En esta orden, hacemos lo contrario al read, ahora
vamos a escribir el resultado guardado en la variable
area, para ello usamos la orden write
y en este caso el primer asterisco indica “donde estoy”, es decir mi
pantalla y el segundo asterisco sin un formato, o sea todos los
decimales. Lo que escribimos en la pantalla (o un printer) a
continuación, y es el texto ´El area es =´ y luego el valor guardado en
la variable area.
Por ejemplo, podríamos obtener como resultado el siguiente texto: El
area es = 23.45566
La sentencia end es para avisar al compilador cuando
crea el código ejecutable que el programa terminó.
Para compilar este programa, en linux escribimos: gfortran triangulo.f -o triangulo donde triangulo.f sería un archivo de texto que contuviese el programa que hemos analizado. El “-o” indica el nombre del programa ejecutable que se debe crear, en este caso “triángulo”.
Este capítulo es sólo para dar una vista rápida de los modos básicos
de las sentencias que manejan los sistemas de lectura y escritura de
datos. Esto es con respecto al ingreso de datos por teclado, su lectura
de una unidad de almacenamiento (disco rígido, SSD, Pen drive, etc),
adquiridos de un dispositivo conectado a la computadora o que se decida
guardar datos en forma permanente. Lo que normalmente serían las órdenes
de entrada/salida (Input/Output en inglés o con sus iniciales I/O de
datos de un programa)
Más adelante en un capítulo especial sobre este tema veremos estos
comandos con mucho más detalle (Cap. 9)
Para la lectura de datos se utiliza la sentencia READ (leer en
inglés). Esta orden en su versión más simple, necesita muy pocos
parámetros para que realice su trabajo. Hay que determinar de dónde se
lee, como se lee y que se lee. La sentencia en su forma mínima podría
escribirse asi:
READ(*,*) A,B,C,D
El primer “*” es la Unida Lógica normalmente es un
número que indica de donde se lee, si tengo un “*” es que se leerá del
teclado en el lugar donde se está corriendo el programa. Es decir, de
ahí se leerán los números que se escriban. En el caso del ejemplo, tengo
que leer 4 variables, así que la computadora esperará que se escriban 4
números separados por al menos un blanco (barra espaciadora), terminando
el ingreso al apretar la tecla de retorno (return o enter según el
teclado).
El segundo “*” indica como se lee, es decir la cantidad de decimales. Lo
habitual es que en ese lugar se escriba un número, y que ese número
indique donde se encuentra una sentencia que se llama FORMAT en la cual
se puede definir la cantidad de lugares que ocupa el número o si hay que
saltear espacios, o bien que tipo de número estoy leyendo (entero, real,
etc). Mas adelante, discutiremos esta sentencia y sus comandos. En este
caso particular que no hay un número y está el “*” con lo cual se cede
la decisión a la computadora para realizar este trabajo. Por lo cual la
cual leerá todos los dígitos decimales encuentre para cada número y
considerará que los números son separados por blancos. Si hubiese más
números que variables para leer los números restantes se ignorarán. si
se escriben menos números y se apreta la tecla de entrada, el programa
seguirá esperando que se completen la cantidad de números restantes para
que cada variable tenga un valor ingresado.
La sentencia WRITE realiza la función contraria del READ. Con ella
podemos escribir el resultado de un programa en el sistema de
almacenamiento, en la pantalla o quizás en una impresora. Se usa de una
forma similar a la sentencia READ:
WRITE(*,*) X,Y,Z
El primer “*” de la sentencia READ, es la Unida
Lógica y es una indicación del lugar donde escribo, normalmente
un número6. Este número identifica un archivo,
la impresora, mi monitor, etc. Si hay un “*” o un “1” el lugar donde se
escribirán las variables es la pantalla de donde se está corriendo el
programa. En este caso, se imprimirán los números que están guardados en
las variables X,Y,Z separadas por un espacio.
El segundo “*” es el formato (FORMAT) y funciona en forma similar a como
lo indicamos en la sección de la sentencia READ. En este caso se
imprimirán todos los decimales de los números.
Los archivos (files en inglés) son la unidad de almacenamiento en los discos rígidos y demás sistemas que guardan información en forma permanente. Los archivos se localizan en directorios cuya función es la organización de la información. En cada directorio sólo puede existir un solo archivo con un nombre determinado, es decir no puede repetirse el mismo nombre en otros archivos para un dado directorio, pero si puede estar un archivo con nombre similar en otros directorios. En la mayoría de los sistemas operativos, los directorios pueden contener otros directorios y estos a su vez más directorios.
Las reglas sobre los nombres y tamaños de los archivos están dadas por el File System que es la definición de cómo se formateó el disco (ver capitulo 1). Hay que recordar que los Sistemas Operativos, pueden manejar varios tipos de File Systems, por ejemplo en la actualidad la mayoría de los pen-drives vienen formateados de fábrica con el File System FAT32 y aunque es un sistema de formateo de la empresa Microsoft, tanto el Linux, como el MacOSX (Apple) lo pueden leer. Incluso las máquinas fotos suelen usar este formato que es uno de los más comunes en las tarjetas de memoria.
Para leer o escribir un archivo secuencial (el tipo más usado) se usa
la sentencia OPEN().
OPEN(22, fiile=’estrellas.dat’)
READ(22,*) X1,X2,X3
Es decir leo un renglón y los tres número que leo los asigno a las
variables X1,X2,X3
Pero también puedo escribir sobre otro archivo haciendo:
OPEN(35, fiile=´salida.txt´)
WRITE(35,*) A,B
Donde aquí escribo sobre el archivo salida.txt
La sentencia DO permite la repetición de un cálculo
modificando uno de sus parámetros en forma controlada. Para realizar la
tarea se establece un valor de inicio, un valor final y un paso que
delimita los valores en los cuales el parámetro tomará valores. Pero
mejor, veámoslo con un ejemplo: quiero calcular la suma de la siguiente
serie:
\[S = \sum_{i=1}^{N} 1/i^{2}\]
donde N podría ser incluso número muy grande. Como
vemos el término \(1/i^{2}\) se calcula
repetidamente al hacer las cuentas. Si quisiera hacer un programa
tendría que repetir una y otra vez este término cambiando el valor de
i, lo cual sería muy un trabajo muy arduo además de
tedioso. Sin embargo, la fórmula que define la serie es compacta y para
la variable i se establece que toma todos los valores
desde i = 0 hasta i = N
Lo que se hace con la sentencia DO es escribir la
fórmula en una manera muy parecida a la notación matemática usual, es
decir la que se utiliza para describir la sumatoria como en este
caso.
Un programa que haga este cálculo se podría escribir con mucha
simplicidad y quedaría:
C Programa para realizar el calculo de la suma de la Serie
finita i**2
\(\ \ \ \ \ \ \ \) Program
Suma
\(\ \ \ \ \ \ \ \) write(*,*)
’¿Cuantos términos quiero sumar?’
\(\ \ \ \ \ \ \ \) read(*,*)
N
\(\ \ \ \ \ \ \ \)
suma=0.
\(\ \ \ \ \ \ \ \) DO i=1, N
\(\ \ \ \ \ \ \ \ \ \ \) x = i ! i es entero. No quiero que las operaciones se realicen en números enteros7
\(\ \ \ \ \ \ \ \ \ \ \) suma = suma + 1/ x**2
\(\ \ \ \ \ \ \ \)
ENDDO
\(\ \ \ \ \ \ \ \) write(*,*)
’La suma de la serie es =’, suma
\(\ \ \ \ \ \ \ \)
end
En este programa, vemos que se ingresa el valor de N,
que es el número que indica la cantidad de términos de la serie que se
van a sumar. Luego se asigna el valor 0 en la variable
suma8. Esta variable irá acumulando la
suma parcial de los términos calculados. Luego se ejecuta la orden
DO que actúa sobre la variable i ¿Cómo
lo hace?
La variable i va a tomar primero el valor 1, porque en
el DO se indica que es es el comienzo, y su último
valor será el valor de N. Como no se indica el paso
este será 1. Entonces i comenzará valiendo 1 y se
realizará el cálculo hasta el ENDDO, luego con
i=2 y se calculará de nuevo, luego las operaciones se
repetirán con i=3, así hasta lleguemos a que
i tome el valor N. En el próximo ciclo
i valdrá N+1, entonces al haber pasado
el valor límite ya no continuará el cálculo y continuará ejecutando las
sentencias después del ENDDO. Que para nuestro caso en
particular es escribir en pantalla el resultado de la suma de la
serie.
Hay varias cosas para señalar, la primera es que valor final de
i al terminar será N+1, ya que el
sistema sumará un 1 a i y descubrirá que ya se pasó del
valor límite que es N, por lo cual no continuará el
cálculo.
La segunda, es que el tiempo que la computadora tardará en hacer el
cálculo es lineal con N para este caso en particular.
Para un N más grande, más tarda el programa. Si
determino el tiempo que tarda para \(N=100\) con este tiempo podré estimar el
tiempo que tardará para cualquier otro valor de \(N\). Ya que: \(\mathbf{tiempo \propto N}\)
Y la tercera, es que el programa fue escrito a un nivel abstracción en
el cual sólo hay que indicar cuantos términos de la serie quiero y el
sistema los calcula sin modificar el código. Es decir, mi programa sólo
depende de ingresar el N y da lo mismo si la serie
tiene pocos términos o muchos, no hay que modificar el programa ni
re-compilarlo. Como punto importante a señalar, es que muy fácilmente
puedo construir un programa cuya ejecución supere cualquier tiempo
razonable para que la computadora lo finalice, o peor no termine
nunca.
La sentencia DO se escribe:
DO variable=inicio, final, paso
En inicio, final y paso podemos poner un número, una variable (se
utiliza el valor que se guarda en esa variable, como en el ejemplo
anterior) o una fórmula (la cual se calculará y el resultado se usará
como el valor en cuestión). En general se considera, que se puede poner
en el inicio, final y paso expresiones matemáticas. Un valor constante
es la expresión matemática más simple. Si no ponemos el paso, este se
considerará 1, este es el valor por default9
El paso puede ser negativo, en cuyo caso el inicio debe ser una número mayor al numero final y se hará un cálculo con números que van decreciendo. Inicio, final y paso pueden ser números reales, pero hacer esto es desaconsejado porque por pérdida de decimales podría en algún caso que se realice un loop de menos o de más de lo que se pensó hacer. Por ejemplo, se programa el final con el número real 4.0 pero el calculo da que la variable del DO en vez de 4.0 da 3.9999999 entonces se repetiría un loop de más que el programador nunca quizo hacer y quizás le arruine el cálculo.
La variable que es el parámetro de un DO no puede
ser modificada por ningún cálculo dentro del propio DO,
si puede una vez que el DO ha finalizado. Sólo son
posibles las modificaciones indicadas en la sentencia
DO a través de la definición (inicio, final y paso) que
se le da a la variable. Intentar cambiar el valor de este variable será
indicado como error y en la mayoría de los casos por el propio
compilador.
Puede existir un o varios DOs dentro de otro, pero
sobre una variable diferente, ejemplo:
\(\ \ \ \ \ \ \ \) DO i=1, N
\(\ \ \ \ \ \ \ \ \ \ \) DO j=1, N
\(\ \ \ \ \ \ \ \ \ \ \) Varias sentencias con cálculo
\(\ \ \ \ \ \ \ \ \ \ \) ENDDO
\(\ \ \ \ \ \ \ \)
ENDDO
Una sentencia equivalente al DO existe en todos los
lenguajes de computación, muchas veces con otro nombre, pero su uso es
similar. Una cantidad importante de lenguajes la escriben como
for y con parámetros similares al Fortran. En algunos
lenguajes el paso no solamente puede ser aditivo, sino que ademas hay
opciones para que sea geométrico (multiplicativo), que siga una ley de
potencias o que sea logarítmico.
Dato importante: toda fórmula matemática a calcular del
tipo sumatoria, productoria, operaciones con subíndices como por ejemplo
cálculos con matrices, claramente es un DO obligado al
programarla en Fortran.
Por ejemplo, el segmento de un programa que calcule el factorial de un
número N y guardarlo como resultado en una variable llamada F
sería:
\(\ \ \ \ \ \ \ \)
\(\vdots\)
\(\ \ \ \ \ \ \ \ \ \ \) F=1.
\(\ \ \ \ \ \ \ \ \ \ \) DO i=1,N
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \) F = F * i
\(\ \ \ \ \ \ \ \ \ \ \) ENDDO
\(\ \ \ \ \ \ \ \)
\(\vdots\)
Donde ahora estamos usando a la variable F para primero cargarle un 1.
(el elemento neutro del producto), luego los resultados parciales y por
último quedaría el factorial del número.
Calcular la tabla de numérica que se produce de la siguiente
fórmula:
\(F = 2n + m\) y n
toma valores en el rango n=2,4,6,8...20 y
m los toma tal
m=1,2,3,4,...,n
Vemos que n toma los pares hasta el 20 (de esta información se deduce
el inicio, final y el paso de la secuencia), mientras que
m comienza en 1, tiene paso 1, pero finaliza en
n. Con esta información se debería hacer:
\(\ \ \ \ \ \ \ \) Program
Tabla
\(\ \ \ \ \ \ \ \) integer F
\(\ \ \ \ \ \ \ \) write(*,*) ’ N M F’
\(\ \ \ \ \ \ \ \) DO n=2,20,2
\(\ \ \ \ \ \ \ \ \ \ \) DO m=1,n
\(\ \ \ \ \ \ \ \ \ \ \ \ \) F= 2*n+m
\(\ \ \ \ \ \ \ \ \ \ \ \ \) write(*,*) n,m,F
\(\ \ \ \ \ \ \ \ \ \) ENDDO
\(\ \ \ \ \ \ \ \ \) ENDDO
\(\ \ \ \ \ \ \ \)
END
Como se puede apreciar en este ejemplo, el DO más
externo controla la variable n, la cual es parte de la
definición del rango de números del DO mas interno (el
de m). Por ello, cuando crece n, crece
también la cantidad de loops que el DO mas interno está
obligado a realizar. Esto es un ejemplo de la importante variedad de
situaciones que se pueden programar con esta sentencia.
El problema de la pérdida de decimales debido a que los números no
tienen infinitos decimales en su representación binaria en la
computadora lo hemos comentado pero no hemos visto ejemplos donde esta
situación nos pueda perjudicar. Este problema puede tener un efecto
negativo en cálculos largos o que se realicen sobre programas donde sus
algoritmos propagan inadecuadamente los errores (por ejemplo, sistemas
donde las perturbaciones crecen en magnitud a medida que se realizan más
operaciones matemáticas).
El programa que calcula la serie que discutimos al principio de este
capítulo puede servirnos para visualizar el efecto que se produce al
perder constantemente los decimales menos significativos en cada
operación matemática que se hace. En un principio, esta pérdida puede
aparentar ser una pérdida muy menor, su acumulación como un error de
cálculo sistemático puede afectar los resultados finales. Si bien,
también hay que considerar que en la mayoría de los cálculos este efecto
no suele ocurrir, pero no por eso hay que dejar de estar conscientes de
su existencia. Ya que cuando ocurre podemos estar en el caso de realizar
un cálculo muy complejo o largo y por lo tanto obtener resultados
incorrectos al final de este.
El programa anterior calcula la sumatoria de la serie con término
\(1/i^2\) y al tener en el denominador
un término cuadrático este provoca que al crecer el valor de \(i\) los términos de la serie sean números
cada vez más pequeños. Vamos a aprovechar esta situación para visualizar
el problema. Como la serie no es mas que una suma, es equivalente
calcularla de dos maneras: sumándola desde el principio (desde \(i=1\), hasta N, con paso 1) o haciéndola
desde el final (empieza en \(i=N\), con
paso -1, y termina cuando \(i= 1\) como
valor final).
En Fortran podemos hacer ambos cálculos con sólo cambiar sentencia DO
del programa que vimos como ejemplo anteriormente. Es decir podríamos
calcular usando:
DO i=1,N o DO i=N,1,-1 y ambos métodos
deberían dar el mismo resultado. Pero además, hay que recordar que la
serie converge al infinito:
\[S = \sum_{i=1}^{\infty} 1/i^{2} = \pi^2/6 \sim 1.64493406684822643\]
Con lo cual tenemos el valor al cual converge la serie en el infinito y por lo tanto una referencia con la cual comparar los números obtenidos con distintos N. Con la ventaja de que usaremos N grandes y entonces los resultados deberían parecerse a este número. Con este valor puedo estimar la precisión del resultado que estoy obteniendo y al mismo tiempo comparar este resultado contra los dos métodos de cálculo. La idea es que al sumar más términos de la serie, veamos si los errores en los cálculos aumentan por tener una cantidad finita de decimales o no, ya que podemos contrastar el resultado contra la suma exacta. También podremos ver si hay diferencia entre ambos métodos: la suma creciente y la suma decreciente.
Veamos en la tabla 6.1 los resultados de las corridas del programa para distintos valores de N en ambos cálculos, es decir con i creciente hasta N y con i decreciendo desde N.
| N | Resultado i creciendo | Error | Resultado i decreciendo | Error |
|---|---|---|---|---|
| 100 | 1.63498402 | 9.95016098E-03 | 1.63498390 | 9.95028019E-03 |
| 1000 | 1.64393485 | 9.99331474E-04 | 1.64393449 | 9.99689102E-04 |
| 10,000 | 1.64472532 | 2.08854675E-04 | 1.64483404 | 1.00135803E-04 |
| 100,000 | 1.64472532 | 2.08854675E-04 | 1.64492404 | 1.01327896E-05 |
| 1,000,000 | 1.64472532 | 2.08854675E-04 | 1.64493299 | 1.19209290E-06 |
| 10,000,000 | 1.64472532 | 2.08854675E-04 | 1.64493394 | 2.38418579E-07 |
| 100,000,000 | 1.64472532 | 2.08854675E-04 | 1.64493406 | 1.19209290E-07 |
Para pensar:
¿Por qué la suma decreciente da mejor resultado?
¿Cuál sería la manera de mejorar este cálculo, con el fin de disminuir
este efecto?
El uso de la sentencia DO en el caso de vectores y matrices es muy
útil, ya que es la herramienta adecuada para controlar los subíndices de
los elementos que forman estas estructuras. Veamos varios
ejemplos:
Cargar una matriz en memoria y sumar los cuadrados de sus elementos de
la diagonal.
Como la diagonal para una matriz con elementos \(a_{i,j}\) son los elementos cuyos indices
\(i\) y \(j\) son iguales, la suma de la diagonal
sería:
\[S = \sum_{i=1}^{N} a_{i,i}\]
En el programa primero definiré el tamaño de la máximo matriz, luego
leeré de pantalla cuál es su tamaño real (n). Con este valor de n puedo
construir dos DOs. El primero genera todos lo casos posibles \(i\) y el segundo todos los casos de \(j\). De esta manera puedo leer de pantalla
elemento a elemento de la matriz. Una vez que leí todos los elementos,
puedo pasar a realizar el cálculo.
\(\ \ \ \ \ \ \ \) program
diagonal
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \) real*4 a(100,100)
\(\ \ \ \ \ \ \ \) read(*,*) n. ! leo el tamaño de la matriz
\(\ \ \ \ \ \ \ \) do i=1,n
\(\ \ \ \ \ \ \ \ \ \) do j=1,n
\(\ \ \ \ \ \ \ \ \ \ \ \) read(*,*) a(i,j) ! leo los elementos
\(\ \ \ \ \ \ \ \ \ \) enddo
\(\ \ \ \ \ \ \ \) enddo
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \) tn=0.
\(\ \ \ \ \ \ \ \) do i=1,n
\(\ \ \ \ \ \ \ \ \ \ \) tn=tn+a(i,i) ! Hago el cálculo
\(\ \ \ \ \ \ \ \) enddo
\(\ \ \ \ \ \ \ \) write(*,*) ’la suma de la diagonal es =’, tn. ! imprimo el resultado
\(\ \ \ \ \ \ \ \)
end
Probemos ahora sumar los elementos de la diagonal multiplicada por su
antidiagonal, esta sería: \[S =
\sum_{i=1}^{N} a_{i,i}\ a_{i,n-i+1}\]
Y si tomo la parte que hace solo la operación (la lectura será igual
que en el programa anterior)
\(\ \ \ \ \ \ \ \) program
antidiagonal
\(\ \ \ \ \ \ \ \) \(\vdots\) ! Cargo los datos de la Matriz A
\(\ \ \ \ \ \ \ \) tn=0.
\(\ \ \ \ \ \ \ \) do i=1,n
\(\ \ \ \ \ \ \ \ \ \) tn=tn+a(i,i)*a(i,n-i+1) ! hago el cálculo del subíndice (N-i+1) y lo utilizo
\(\ \ \ \ \ \ \ \) enddo
\(\ \ \ \ \ \ \ \) write(*,*)’la suma de la diagonal por la antidiagonal es=’, tn
\(\ \ \ \ \ \ \ \)
end
Para sumar los elementos de las filas, tomo el índice de la fila y
uso una sentencia DO que recorra toda la fila y un DO externo que
recorra a su vez todas las filas de la Matriz. El resultado de esta
operación un vector por lo cual tengo que definirlo.
\(\ \ \ \ \ \ \ \) PROGRAM
FILA
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \) REAL*4 A(100,100),R(100))
\(\ \ \ \ \ \ \ \) \(\vdots\) ! Cargo los datos de la Matriz A
\(\ \ \ \ \ \ \ \) \(\vdots\)
\(\ \ \ \ \ \ \ \) DO I=1,N
\(\ \ \ \ \ \ \ \) R(I)=0.
\(\ \ \ \ \ \ \ \ \ \) DO J=1,N
\(\ \ \ \ \ \ \ \ \ \ \ \ \) R(I) = R(I) + A(I,J)
\(\ \ \ \ \ \ \ \ \ \) ENDDO
\(\ \ \ \ \ \ \ \) ENDDO
\(\ \ \ \ \ \ \ \) \(\vdots\) ! Escribo el resultado del Vector R
\(\ \ \ \ \ \ \ \)
END
En donde se puede ver la versatilidad de este tipo de comando es en
la multiplicación de matrices
Si tengo dos matrices A y B de igual tamaño) y las multiplico con
resultado C, o sea:
\(A x B = C\)
Es decir
\[\begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} & \cdots & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & \cdots & a_{2,n} \\ a_{3,1} & a_{3,2} & a_{3,3} & \cdots & a_{3,n} \\ %a_{(4,1)} & a_{(4,2)} & a_{(4,3)} & a_{4,4} & . & . & . \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ % .& .&.&.&.\\ % .& .&.&.&.\\ a_{n,1} & a_{n,2} & a_{n,3} & \cdots & a_{n,n} \\ \end{bmatrix} x \begin{bmatrix} b_{1,1} & b_{1,2} & b_{1,3} & \cdots & b_{1,n}\\ b_{2,1} & b_{2,2} & b_{2,3} & \cdots & b_{2,n} \\ b_{3,1} & b_{3,2} & b_{3,3} & \cdots & b_{3,n} \\ %a_{(4,1)} & a_{(4,2)} & a_{(4,3)} & a_{4,4} & . & . & . \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ % .& .&.&.&.\\ % .& .&.&.&.\\ b_{n,1} & b_{n,2} & b_{n,3} & \cdots & b_{n,n} \\ \end{bmatrix} = \begin{bmatrix} c_{1,1} & c_{1,2} & c_{1,3} & \cdots & c_{1,n}\\ c_{2,1} & c_{2,2} & c_{2,3} & \cdots & c_{2,n} \\ c_{3,1} & c_{3,2} & c_{3,3} & \cdots & c_{3,n} \\ %a_{(4,1)} & a_{(4,2)} & a_{(4,3)} & a_{4,4} & . & . & . \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ % .& .&.&.&.\\ % .& .&.&.&.\\ c_{n,1} & c_{n,2} & c_{n,3} & \cdots & c_{n,n} \\ \end{bmatrix}\]
Donde elemento de C se calcula como:
\[C_{i,j} = \sum_{k=1}^{N} A_{i,k} B_{k,j}\]
Esta formula es muy sencilla de programar tomando en cuenta que ahora
tengo tres variables (i, j y k), las cuales tienen que tomar todos sus
valores posibles dentro del programa para realizar el cálculo total. Una
de ellas (k) tiene que hacer un ciclo completo para
cada i y j. Veamos como sería el
programa que resuelve este problema (obviamos la carga de datos en
memoria de cada matriz para no hacer tan largo el código)
\(\ \ \ \ \ \ \ \) PROGRAM
PRODUCTO
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \) REAL*4 A(100,100),B(100,100),C(100,100)
\(\ \ \ \ \ \ \ \) \(\vdots\) ! cargamos los datos en las matrices A y B
\(\ \ \ \ \ \ \ \) \(\vdots\)
\(\ \ \ \ \ \ \ \) DO I=1,N
\(\ \ \ \ \ \ \ \ \ \) DO J=1,N
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \ \ \ \ \mathbf{ C(I,J)=0}\)
\(\ \ \ \ \ \ \ \ \ \ \) DO K=1,N
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{C(I,J)= C(I,J) + A(I,K) * B(K,J) }\)
\(\ \ \ \ \ \ \ \ \ \ \) ENDDO
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \ \) ENDDO
\(\ \ \ \ \ \ \ \) ENDDO
\(\ \ \ \ \ \ \ \) \(\vdots\) ! Guardamos el resultado de la matriz C
\(\ \ \ \ \ \ \ \) \(\vdots\)
\(\ \ \ \ \ \ \ \)
END
Consideraciones sobre este programa:
Es independiente del tamaño de las matrices salvo que sean más grandes que la dimensión de 100x100 con que se las definió al comienzo del programa. Con cambiar esos números, y re-compilando el problema es fácilmente resuelto. El algoritmo en si, no cambia con el tamaño de las matrices ( “N”).
El tiempo que tarda puede ser importante, como son tres DOs uno dentro de otro el tiempo que tarda es proporcional a \(\mathbf{t \propto N^3}\). Por lo tanto, el tiempo aumenta muy rápido si se incrementa el tamaño de las matrices.
En algoritmos como este cuyo tiempo depende de una potencia de N. Es muy fácil programar algo sencillo que exceda la capacidad de la computadora. Siempre hay que evitar que el tiempo que el programa tarda en correr y entregar un resultado no sea excesivo. Por lo cual, hay que estar atento a si el tiempo es proporcional a una potencia de la cantidad de valores a procesar y cuál es esta potencia. Es decir, se deben elegir cuando sea posible los algoritmos en los cuales esa potencia sea baja. Hay veces que se prefiere un cálculo aproximado a uno que da un resultado exacto pero que consume mucho tiempo en el cálculo.
Reforzando el punto anterior, hay que considerar que realizar más operaciones matemáticas puede hacer que se pierdan más decimales y por lo tanto un cálculo largo tiene una mayor probabilidad a generar resultados que no son del todo correctos o son poco fiables.
La sentencia IF() permite hacer una pregunta y tomar decisiones a partir de la respuesta obtenida a dicha interrogación. Esta posibilidad es extremadamente útil cuando se plantean cálculos a resolver dónde los resultados de ciertas operaciones indican y permiten la elección de las fórmulas y algoritmos matemáticos para la solución del problema. Por lo cual puedo hacer una pregunta sobre ciertas variables y a partir de esa respuesta elegir el camino que sigue el programa. Por ejemplo, en resolución de una ecuación de segundo grado si el discriminante (\(B^2-4AC\)) es menor que cero, la solución está en el campo de los números complejos y no en la de los reales, por lo cual se deben tomar previsiones para este caso. Otro ejemplo, mucho más complicado podría darse si se están calculando modelos de la estructura de una estrella, para cierta capa a una profundidad dada podría haber sólo transferencia de energía por radiación o por convección según la física local (presión, temperatura, etc). Con lo cual el programa podría evaluar esas variables y decidir la física a utilizar.
Hay 3 formas distintas de usar esta orden. La primera de ellas no la usaremos porque ya es obsoleta (conocida como forma aritmética), nos concentraremos en las dos formas modernas de usarla: Esto es: el IF() sentencia y en el IF() en bloque (block if en inglés).
El IF() sentencia funciona haciendo una pregunta a
una expresión o variable, cuyo resultado es una respuesta Booleana, es
decir estamos en el caso que la respuesta a la interrogación es un
Verdadero o un Falso. Se hace la
pregunta y si la respuesta es verdadera se ejecuta la sentencia que está
a la derecha en el mismo renglón que la pregunta. Si es falsa esa orden
escrita a la derecha no se ejecuta y se continua con el programa. La
sentencia tiene esta forma:
IF(algo) sentencia
donde “algo” en su forma más general es una expresión booleana cuya
resolución nos da un resultado verdadero o falso. También podría ser una
variable Lógica sola cuyo valor asignado en el programa sea un verdadero
o un falso.
Si la pregunta tiene que ver con comparar números, se deberán usar los Operadores de Relación.
Estos son: \(>\), \(\geq\), \(=\), \(\neq\), \(<\), \(\leq\) pero como esos símbolos matemáticos no existían en los teclados antiguos, Fortran y otros lenguajes tienen su propia manera de escribirlos, ver tabla 7.1.
| Operador | Escritura en Fortran |
|---|---|
| \(>\) | .GT. |
| \(\geq\) | .GE. |
| \(=\) | .EQ. |
| \(\neq\) | .NE. |
| \(<\) | .LT. |
| \(\leq\) | .LE. |
Ejemplo del uso de IF() com estos operadores:
IF(A.GT.10) A = B**2 + C**2
en este caso estoy indicando que si \(A>10\), el valor de \(A\) cambiará por el cálculo de \(A=B^2+C^2\) de lo contrario seguirá con el
valor que ya tenía asignado.
Es importante volver a notar que la repuesta a la pregunta del
IF() es Booleana, por lo cual nada evita que la haga de
esta manera:
Logical L \(\ \ \ \ \)
! Ahora L es una variable lógica. Esta sentencia tiene que estar al
principio del programa, en la zona donde defino variables.
L= A.GT.10 \(\ \ \) !
Comparo A con 10 y si es cierto guardo en L un verdadero y si no los es
un Falso
IF(L) A = B**2 + C**2 \(\ \ \
\ \) ! Pregunto que sobre L, ya que ahí se guardó el resultado
del cálculo de la expresión anterior que tiene como resultado lógico un
verdadero o un falso.
Para tener una mayor cantidad de opciones existen los Operadores Lógicos. Estos sirven para realizar varias preguntas simultáneas. Ya que permiten comparar distintos resultados lógicos con reglas que impongo a través de estos operadores. A estos operadores los conocen de la asignatura Álgebra I. Recordemos los de uso más común, ver tabla 7.2
| Operador | Fortran | Operación |
|---|---|---|
| Negación | .NOT. | Cambia el valor de la expresión lógica a su opuesto |
| Conjunción | .AND. | Cierto únicamente si ambas expresiones lógicas son ciertas |
| Disyunción Inclusiva | .OR. | Cierto si una de las expresiones es cierta |
| Disyunción exclusiva | .XOR. | Cierto únicamente si una de las expresiones es cierta |
| Equivalente | .EQV. | Cierto si ambas expresiones tienen el mismo valor |
| No equivalente | .NEQV. | Cierto si ambas expresiones no tienen el mismo valor |
El resultado Booleano que uno espera en una expresión lógica, como
hemos visto, puede ser la combinación de una cantidad de operaciones
matemáticas, de relación y por último lógicas. Por lo cual se puede
hacer tabla con el orden de prioridades de cómo estas operaciones son
resueltas. Veamos la tabla 7.3:
| Tipo de Operación | Operador | Asociatividad | Prioridad |
|---|---|---|---|
| Aritmética | ** (potencia) | Derecha a izquierda | 1 |
| *, / | Izquierda a derecha | 2 | |
| +,- | Izquierda a derecha | 3 | |
| Relacionales | .GT., .GE., .EQ., .NE., .LT., .LE. | No tienen | 4 |
| Lógicos | .NOT. | Derecha a izquierda | 5 |
| .AND. | Izquierda a derecha | 6 | |
| .OR. | Izquierda a derecha | 7 | |
| .EQV., .NEQV. | Izquierda a derecha | 8 |
El IF sentencia tiene una limitación muy importante y es que si la
condición se cumple sólo puede ejecutar una sola orden y no más.
Históricamente forma de programar se la ha combinado con una sentencia
llamada GOTO y suele considerarse como una muy manera
poco feliz de realizar programas, ya que los códigos escritos de esta
forma son muy confusos y difíciles de modificar. La orden GOTO funciona
de la siguiente manera:
\(\ \ \ \ \ \ \ \)GOTO
99
\(\ \ \ \ \ \ \ \ \vdots\) se saltean estas líneas
\(99 \ \ \ \ \ \)sigue el
programa...
Cuando la ejecución de un programa encuentra la orden
GOTO en vez de seguir con la sentencia que está debajo
salta a la que tiene la etiqueta (99). Esta etiqueta puede ser una
sentencia posterior o incluso anterior a la que está el
GOTO.
Esta orden tiene en si una utilidad, por ejemplo, para romper un ciclo
DO de la siguiente manera: si en un cálculo tengo
programados un bucle DO muy largo y descubro que no necesito terminarlo,
porque el resultado ya esta calculado (ejemplo: una serie convergió muy
rápido) puedo preguntar si esto pasó y escapar del DO
antes que termine y ahorrar un montón de tiempo de computación.
Así:
\(\ \ \ \ \ \ \ \)DO
i=1,100000
\(\ \ \ \ \ \ \ \) \(\vdots\)
\(\ \ \ \ \ \ \ \)IF (algo) GOTO 20
\(\ \ \ \ \ \ \ \) \(\vdots\)
\(\ \ \ \ \ \ \ \)ENDDO
20 \(\ \ \ \)CONTINUE
\(\ \ \ \)sigue el
programa...
Ejemplo: cálculo la serie de Taylor de la función cos(x), con un error
menor a \(error < 10^{-6}\)
\[Cos(x) = \sum_{i=0}^\infty \frac{
(-1)^{i}x^{2i}}{(2i)!} = 1 - \frac{x^2}{2!} +
\frac{x^4}{4!}-\frac{x^6}{6!} + ... + \lvert error(\xi)
\rvert\]
Veamos el programa:
El programa es simple, vamos calculando los términos de la serie y
sumándolos, pero al mismo tiempo calculamos el término del error.
Evaluando ese término sabemos si llegamos al valor del error que
requerimos. Si no llegamos a satisfacer la condición de tener un error
más pequeño del que establecimos como satisfactorio, calculamos un
término más a la serie y continuamos el proceso. Pero si obtenemos un
error que nos determina que ya calculamos un valor útil para nuestras
necesidades, el IF() nos permite terminar el programa y no hacer más
cálculos innecesarios consumiendo recursos de la computadora.
\(\ \ \ \ \ \ \ \) Program
cos_de_angulo 10\(^{,}\)11
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \) write(*,*) ’ingrese el valor del ángulo n’
\(\ \ \ \ \ \ \ \) read(*,*) omega
\(\ \ \ \ \ \ \ \) pi=3.14159265358979
\(\ \ \ \ \ \ \ \) omega=omega/180*pi
\(\ \ \ \ \ \ \ \) xmax=pi/2
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \) coseno=0
\(\ \ \ \ \ \ \ \) do i=0,1000000
\(\ \ \ \ \ \ \ \ \ \)
C\(\ \ \ \ \ \ \ \) Calculo el factorial para el término y para del error: n! y (n+2)!
\(\ \ \ \ \ \ \ \ \ \) facto=1.
\(\ \ \ \ \ \ \ \ \ \) do ii=1,2*i
\(\ \ \ \ \ \ \ \ \ \ \ \) facto=facto*ii
\(\ \ \ \ \ \ \ \ \ \) enddo
\(\ \ \ \ \ \ \ \ \ \) facto2=facto*(i+1)*(i+2)
\(\ \ \ \ \ \ \ \ \ \)
C\(\ \ \ \ \ \ \ \) Calculo el termino i
\(\ \ \ \ \ \ \ \ \ \) term=omega**(2*i)*(-1)**(i)/facto
\(\ \ \ \ \ \ \ \)
C\(\ \ \ \ \ \ \ \) Calculo el término y el error
\(\ \ \ \ \ \ \ \ \ \) coseno=coseno+term
\(\ \ \ \ \ \ \ \ \ \) eterm= xmax**(2*i+2)/facto2
\(\ \ \ \ \ \ \ \)
C\(\ \ \ \ \ \ \ \)Pregunto si llegué al error deseado
\(\ \ \ \ \ \ \ \ \ \) if(eterm.LT.1E-8) goto 99
\(\ \ \ \ \ \ \ \) enddo
\(\ \ \ \ \ \ \ \)
99\(\ \ \ \ \ \ \ \) write(*,*) i, coseno, cos(omega)
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)
end
El IF utilizado como bloque permite subsanar la
deficiencia que tiene el IF sentencia de que sólo permite la ejecución
de una sola orden, con este comando es posible realizar una serie muy
larga de órdenes . Funciona de esta manera:
IF (expresión lógica) THEN
sentencia 1
sentencia 2
...
ELSEIF(expresión lógica 2) THEN
sentencia
sentencia
...
ELSEIF(expresión lógica 3) THEN
sentencia
sentencia
....
ELSE
sentencia
sentencia
...
ENDIF
¿Cómo funciona esta estructura de órdenes?
La primera sentencia sólo se diferencia del caso anterior porque a su
derecha está la palabra THEN que le indicaría al
compilador que estamos en el caso del IF() en bloque y
no en el caso anterior del IF() sentencia. Esta orden se podría traducir
al lenguaje coloquial como: Si pasa esto entonces hacemos todo esto
que sigue y pero si no pasó esto pero pasó esto otro hacemos todas estas
otras cosas. Y en cada caso lo que se hace no es ejecutar una sola
orden sino todo un conjunto de órdenes sin límite de cantidad. Pueden
escribirse todas las preguntas diferentes que se necesiten para resolver
el problema. Veámoslo con más detalle:
Viendo el esquema, si la primera expresión lógica es verdadera se
cumplen la sentencia 1, luego la 2 y así hasta que estas se acaban. Si
la pregunta dio como resultado un verdadero, todas las órdenes que
siguen se saltean y luego el programa continua su ejecución después del
ENDIF.
Si la expresión lógica es falsa. Se continua con las siguientes
preguntas en orden. Si la expresión lógica de primer
ELSEIF es cierta se cumplen con las sentencias
asociadas a este ELSEIF() y luego el programa continua
con las sentencias que siguen al ENDIF. Si la expresión
lógica no es cierta, se pregunta si es cierta la del segundo
ELSEIF() y así sucesivamente con todos los
ELSEIF() que hayan. Si ninguna de las expresiones del
IF() o de los ELSEIF() son verdaderas,
y sólo si en ese caso, se activan las sentencias del
ELSE final. Este actúa en la forma de que solo se
cumplen las sentencias debajo de él en el caso de que ninguna pregunta
que se haya hecho haya sido verdadera.
Salvo la orden inicial IF() THEN y la última
ENDIF todas las demás sentencias internas pueden o no
estar. Nada impide tener la cantidad de sentencias ELSEIF()
THEN que se requieran para la tarea, o ninguna. Y en el caso
del ELSE si lo lógica de lo que está programando no lo
necesita esta orden no se la utiliza y por consiguiente no se la
escribe. Básicamente el IF en bloque es una estructura
de módulos de los cuales se eligen los que se requieran para la resolver
la tarea.
Ejemplos:
Función a trazos
Supongamos que en alguna parte de un programa, deberíamos calcular la
siguiente función a trazos:
\[\label{eq:funcion_a_trozos} f(x) = \left\{ \begin{array}{ll} 0 & \mathrm{si\ } x \le 30 \\ x - 30 & \mathrm{si\ } 30 < x < 60 \\ 30 & \mathrm{si\ } 60 \le x \end{array} \right.\]
La parte del programa que hace este trabajo tendría la siguiente
forma:
\(\vdots\)
IF (X.LE.30) THEN
\(\ \ \ \ \ \ \ \) F =
0
ELSEIF(X.GT.30.AND.X.LT.60) THEN
\(\ \ \ \ \ \ \ \) F = X -
30
ELSE
\(\ \ \ \ \ \ \ \) F =
30
ENDIF
\(\vdots\)
Es decir, primero se verifica que \(X \leq
30\). Si la pregunta es cierta se ejecuta la orden \(F=0\) y se termina la sentencia
IF. Si no lo es, se pregunta si \(30 < x < 60\) y si es veraz, corre F
= X - 30 y se termina el IF. Si tampoco es verdadera se
ejecuta si o si lo que sigue a la sentencia ELSE que es
\(F= 30\) y se continua con el
programa.
Solución de una ecuación de segundo grado
Resolver una ecuación cuadrática tiene interés porque según sus
coeficientes, los resultados son diversos. Las soluciones pueden ser dos
números reales, el mismo número repetido dos veces, o dos números
complejos. Por lo cual al hacer un programa hay que tomar cuenta estos 3
casos por separado y por lo tanto utilizar la sentencia
IF() para determinar en cual de estas distintas
situaciones se encuentra nuestra solución.
Por lo cual, si mi ecuación es \(AX^2+BX+C =
0\) tengo que ver si \(B^2 - 4 * A*
C\) es mayor que cero (dos raíces reales), igual a cero, o sea
dos raíces iguales, o menor que cero por lo cual las raíces estarán el
campo de los números complejos.
El programa seria:
\(\ \ \ \ \ \ \ \) program cuad
\(\ \ \ \ \ \ \ \) complex z1,z2
\(\ \ \ \ \ \ \ \) read(*,*) a,b,c
\(\ \ \ \ \ \ \ \) disc=b*b-4*a*c
\(\ \ \ \ \ \ \ \) if(disc.lt.0) then
\(\ \ \ \ \ \ \ \ \ \ \ \) z1=(-b+sqrt(complex(disc,0)))/(2*a)
\(\ \ \ \ \ \ \ \ \ \ \ \) z2=(-b-sqrt(complex(disc,0)))/(2*a)
\(\ \ \ \ \ \ \ \ \ \ \ \) write(*,*)’raices complejas:’,z1,z2
\(\ \ \ \ \ \ \ \) elseif(disc.eq.0) then
\(\ \ \ \ \ \ \ \ \ \ \ \) x=-b/(2*a)
\(\ \ \ \ \ \ \ \ \ \ \ \) write(*,*)’ el disc. es cero, x=’,x
\(\ \ \ \ \ \ \ \) else
\(\ \ \ \ \ \ \ \ \ \ \ \) x1=(-b+sqrt(disc))/(2*a)
\(\ \ \ \ \ \ \ \ \ \ \ \) x2=(-b-sqrt(disc))/(2*a)
\(\ \ \ \ \ \ \ \ \ \ \ \) write(*,*) x1,x2
\(\ \ \ \ \ \ \ \) endif
\(\ \ \ \ \ \ \ \)
end
Veremos parte por parte que hace este programa y sobre todo la función
If que en este caso decidirá la forma de resolver la ecuación:
\(\ \ \ \ \ \ \ \) program
cuad
\(\ \ \ \ \ \ \ \) complex z1,z2
Comienza el programa y por las dudas defino dos variables complejas que usaré llegado el caso de tener raíces complejas, en el caso de tenerlas no las utilizaré.
\(\ \ \ \ \ \ \ \) read(*,*) a,b,c
\(\ \ \ \ \ \ \ \) disc=b*b-4*a*c
Leo los coeficientes de las ecuación y calculo el discriminante, el cual determinará el tipo de solución
\(\ \ \ \ \ \ \ \) if(disc.lt.0) then
\(\ \ \ \ \ \ \ \ \ \ \ \) z1=(-b+sqrt(complex(disc,0)))/(2*a)
\(\ \ \ \ \ \ \ \ \ \ \ \) z2=(-b-sqrt(complex(disc,0)))/(2*a)
\(\ \ \ \ \ \ \ \ \ \ \ \)
write(*,*)’Raices complejas:’,z1,z2
este punto del programa, se pregunta: ¿Es el discriminante menor que
cero? Si es así cálculo las dos raíces complejas. Como la solución tiene
una parte imaginaria que proviene de tomar la raíz cuadrada de un número
negativo, debo primero construir ese número como complejo, así la
operación se realizará en el campo de los números imaginarios. Al poner
la orden complex(disc,0)12
estoy convirtiendo la variable disc en un número complejo con parte real
(disc) y parte imaginaria 0, Al hacer esto cualquier operación
matemática de aquí en adelante con este número será en el campo
complejo. Estas operaciones se harán conservando las reglas del álgebra
para números complejos.
De los cálculos z1 y z2 serán las soluciones complejas de la ecuación,
la cuales escribo en la pantalla.
Pero, si el discriminante no es negativo, esta parte del IF no se cumple
y se continua con la siguiente pregunta:
\(\ \ \ \ \ \ \ \)
elseif(disc.eq.0) then
\(\ \ \ \ \ \ \ \ \ \ \ \) x=-b/(2*a)
\(\ \ \ \ \ \ \ \ \ \ \ \) write(*,*)’ el disc. es cero, x=’,x
este caso, si el discriminante es cero, se calcula la solución (en este caso es trivial). Luego se imprime un aviso sobre que caso fue y la solución. Pero si esta pregunta tampoco es cierta si o si estamos en el última caso y se calcula como la solución para raíces reales:
\(\ \ \ \ \ \ \ \ \ \ \ \) x1=(-b+sqrt(disc))/(2*a)
\(\ \ \ \ \ \ \ \ \ \ \ \) x2=(-b-sqrt(disc))/(2*a)
Y luego se imprime el resultado:
\(\ \ \ \ \ \ \ \ \ \ \ \) write(*,*) x1,x2
La sentencia Do While() es la combinación entre el
DO y el IF() y básicamente es hacer un
ciclo de sentencias que se repiten mientras una pregunta sea siempre
VERDADERA. Se escribe de la siguiente manera:
DO WHILE (expresión lógica)
\(\ \ \ \)sentencia 1
\(\ \ \ \)sentencia 2
\(\ \ \ \)sentencia 3
\(\ \ \ \)sentencia 4
ENDDO
Ventajas:
Es muy útil cuando se tiene en claro una pregunta que responder, la más típica de estas es: ¿Llegué con los cálculos que hace el programa que está corriendo a un error menor que cierto número? Por ejemplo, tomemos el caso de una serie de Taylor, donde puedo tener un estimador del error. Si como resultado de esa pregunta, si se ha llegado a un error por el cual no se necesita seguir calculando, rompo el ciclo que calcula la serie de Taylor y por lo tanto, el programa continua con las órdenes siguientes. Pero por otro lado, si no arribé al error óptimo se siguen calculando términos de la serie.
Cuando los incrementos en las variables no son aditivos (sumas o restas) sino fórmulas más complejas.
Los programas son compactos y fáciles de leer.
Detalles a tener en cuenta:
Las variables que son necesarias modificar (incrementar o decrementar) no son controladas por el Do While(), si no que se lo debe programar. Por ejemplo en una serie de término \(i\), debo agregar la sentencia \(i=i+1\) para que en cada bucle se incremente la variable que me permite calcular el próximo término de esta serie. A diferencia del la sentencia Do, donde el comienzo, final y paso están claramente indicados, en el Do While() esto no sucede. El programador debe verificar que en cada bucle se produzca una evolución de las variables que permita llegar a un final del loop.
Un error del programador en la construcción de la pregunta puede hacer que el programa quede trabado en el bucle y la corrida en esta situación no terminaría nunca. Por ejemplo, podría pasar que la serie que se está calculando no converja, con lo cual nunca se podría volverse falsa la pregunta del Do While() y entonces no se saldría del loop que se programó.
Kepler en 1609 publicó las leyes que rigen el movimiento de los
planetas. Estos giran alrededor del Sol en una órbita elíptica, uno de
cuyos focos lo ocupa el Sol, pero no lo hacen con un movimiento
uniforme, sino que el radio vector Sol-planeta barre áreas iguales en
tiempos iguales. La expresión matemática de esta ley para este
movimiento proyectado sobre una circunferencia equivalente es la
ecuación de Kepler:
\(M = E - e\ sen(E)\)
donde:
M es la anomalía media o ángulo que recorrería un planeta ficticio que
se moviese con movimiento uniforme si la órbita fuese una circunferencia
cuyo diámetro coincide con el eje principal de la elipse. E es la
anomalía excéntrica (el ángulo real del planeta sobre su órbita elíptica
y e (tal que \(0 \leq e <1\)) es la
excentricidad de la elipse.
M y e se tienen en tablas, pero la posición real del planeta es E, que
es el valor que debemos encontrar.
despejando:
\(E = M + e\ sen(E)\)
El proceso para resolver esta ecuación trascendente se llama iteración13. De tal manera que comienzo con un
valor arbitrario de E (lo llamo E0). Con ese valor y la ecuación
anterior, calculo un nuevo valor de E (lo llamo E1). Este E1 es ahora mi
nuevo E0 para calcular un nuevo valor E1. Si el sistema converge, la
diferencia \(|E1-E0|\) se irá achicando
en cada ciclo y me servirá como cota máxima del error. De esta manera
usando un Do While() puedo repetir el proceso todas las veces que sea
necesario hasta que el valor obtenido tenga un error menor al valor
necesitado.
Veamos un programa que realiza la iteración usando un Do
While()
\(\ \ \ \ \ \ \ \)Program
kepler
\(\ \ \ \ \ \ \ \)real*8 M, E0, E1, exc
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)PI=3.1415926
\(\ \ \ \ \ \ \ \)write(*,*) ’Ingrese el valor de la excentricidad’
\(\ \ \ \ \ \ \ \)read(*,*) exc
\(\ \ \ \ \ \ \ \)write(*,*) ’Ingrese el valor de la Anomalía Media’
\(\ \ \ \ \ \ \ \)read(*,*)
M
\(\ \ \ \ \ \ \ \)M =
M/180*PI
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)E0=0
\(\ \ \ \ \ \ \ \)E1=1
\(\ \ \ \ \ \ \ \)DO WHILE(abs(E1-E0).gt.1e-8)
\(\ \ \ \ \ \ \ \ \ \ \)E0 = E1
\(\ \ \ \ \ \ \ \ \ \ \)E1 = M + exc * sin(E0)
\(\ \ \ \ \ \ \ \ \ \ \)write(*,*) E0,E1,E0-E1
\(\ \ \ \ \ \ \ \)ENDDO
\(\ \ \ \ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \) write(*,*) ’La Anomalía Excéntrica es:’,E1/pi*180,’ Grados’
\(\ \ \ \ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)
end
Si compilo y corro el programa obtengo:
Ingrese el valor de la excentricidad
Ingrese el valor de la Anomalía Media
0.49439150927584963 0.50560849072415037
0.46136377059387018 3.3027738681979446E-002
0.45872439398428766 2.6393766095825222E-003
0.45851154689480583 2.1284708948182685E-004
0.45849437016298522 1.7176731820611746E-005
0.45849298392430504 1.3862386801788418E-006
0.45849287204816341 1.1187614162855297E-007
0.45849286301921632 9.0289470899840296E-009
La Anomalía excéntrica es: 26.269705256849726 Grados
Note que la tercera columna es la cota máxima del error y que esta
disminuye muy rápidamente asegurando un muy buen resultado y en poco
tiempo.
Ejemplo: Vayamos a un problema que ya hemos resuelto, el cálculo la
serie de Taylor de la función cos(x), con un error menor a \(error < 10^{-6}\)
\[Cos(x) = \sum_{n=0}^\infty \frac{
(-1)^{n}x^{2n}}{(2n)!} = 1 - \frac{x^2}{2!} +
\frac{x^4}{4!}-\frac{x^6}{6!} + ... + error(\xi)\]
Veamos el programa
El programa es simple, vamos calculando los términos de la serie y
sumándolos, pero al mismo tiempo calculamos el término de error.
Evaluando ese término sabemos si llegamos al error que necesitamos o no.
Si no llegamos calculamos un término más a la serie y continuamos el
proceso.
\(\ \ \ \ \ \ \
\)
\(\ \ \ \ \ \ \
\)
\(\ \ \ \ \ \ \ \) Program
cos_de_angulo
\(\ \ \ \ \ \ \ \) write(*,*) ’ingrese el valor del ángulo n’
\(\ \ \ \ \ \ \ \) read(*,*) omega
\(\ \ \ \ \ \ \ \) pi=3.14159265358979
\(\ \ \ \ \ \ \ \) omega=omega/180*pi
\(\ \ \ \ \ \ \ \) xmax=pi/4
\(\ \ \ \ \ \ \ \) coseno=0.
\(\ \ \ \ \ \ \ \) eterm=1
\(\ \ \ \ \ \ \ \) i=0
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \) do while(eterm.gt.1e-8)
\(\ \ \ \ \ \ \ \ \ \)
C\(\ \ \ \ \ \ \ \ \ \) Calculo el factorial para el término y para del error: n! y (n+2)!
\(\ \ \ \ \ \ \ \ \ \ \ \) facto=1.
\(\ \ \ \ \ \ \ \ \ \ \ \) do ii=1,2*i
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \) facto=facto*ii
\(\ \ \ \ \ \ \ \ \ \ \ \) enddo
\(\ \ \ \ \ \ \ \ \ \ \ \) facto2=facto*(i+1)*(i+2)
\(\ \ \ \ \ \ \ \ \ \)
C\(\ \ \ \ \ \ \ \ \ \) Calculo el termino i
\(\ \ \ \ \ \ \ \ \ \ \ \) term=omega**(2*i)/facto*(-1)**(i)
\(\ \ \ \ \ \ \ \)
C\(\ \ \ \ \ \ \ \ \ \) Calculo el término y el error
\(\ \ \ \ \ \ \ \ \ \ \ \) coseno=coseno+term
\(\ \ \ \ \ \ \ \ \ \ \ \) eterm= xmax**(2*i+2)/facto2
\(\ \ \ \ \ \ \ \)
C\(\ \ \ \ \ \ \ \ \ \)Incremento i para calcular el término que sigue
\(\ \ \ \ \ \ \ \ \ \ \ \) i = i +1
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \) enddo
\(\ \ \ \ \ \ \ \)
99\(\ \ \ \ \ \ \ \) write(*,*) i,coseno,cos(omega)
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)
end
En este capítulo trataremos los parámetros de las sentencias que
manejan el sistema de lectura y escritura de datos. Es decir, sus usos
al momento del ingreso de datos por teclado, su lectura de una unidad de
almacenamiento (disco rígido, SSD, Pen drive, etc) o la adquisición de
estos de un dispositivo conectado a la computadora. Las sentencias para
el egreso o salida de datos de la computadora tienen sentencias
similares. Si bien para ambos casos, en un capítulo anterior habíamos
visto sus formas más simples.
Los archivos (files en inglés) son la unidad de almacenamiento en los discos y demás sistemas que guardan información en forma permanente. Los archivos se localizan en directorios cuya función es la organización de la información. Hay dos tipos de archivos en FORTRAN, los de acceso secuencial y los de acceso directo.
Como ya hemos visto en un capítulo anterior, estos son los archivos
más comunes en todos los sistemas operativos. De hecho, un programa en
Fortran es un archivo secuencial, lo mismo que su ejecutable una vez
compilado. Cada Byte de información va uno detrás del otro sin
distinción especial de posición o lugar. Son fáciles de manejar y de
usar, pero tienen la desventaja que si se requiere información que está,
por ejemplo, en el medio del archivo tengo que leerlo hasta ese lugar
para encontrar los datos, con la consiguiente pérdida de tiempo. Además
si se escribe un valor en mitad de archivo secuencial ya existente se
borrarán todos los datos desde ese punto en adelante.
Estos archivo tienen renglones de tamaño fijo, este tamaño debe definirse al momento de su creación y es necesario conocerlo para poner leer el archivo14. En estos archivos se puede ir a leer o escribir datos en un renglón en particular sin tener que leer los anteriores. Además se puede escribir en cualquier renglón del archivo sin alterar o borrar los números posteriores a ese punto como sucede en los archivos secuenciales.
Para leer o escribir en un archivo secuencial o directo se usa la
sentencia OPEN(), que trabaja en conjunto
con la sentencia CLOSE() que cierra los
archivos. Open en inglés es abrir y en lenguaje de uso común se habla de
“abrir” cierto archivo. Pero lo que realmente se está haciendo es
indicar que cierto archivo es conectado a una Unidad Lógica especifica
en el programa. Por lo tanto, cada vez que se lee o se escribe apuntando
a esa Unidad Lógica, se lo está haciendo al archivo en particular que la
sentencia OPEN() conectó.
Veamos que significan estos parámetros:
Unidad Lógica (UNIT) es un número que se asigna al archivo que se va leer o escribir. En decir, este número identifica al archivo en cuestión y es utilizado por las sentencias que operan sobre los archivos. La Unidad Lógica se utiliza, por ejemplo, en el READ() o WRITE() para que puedan leer y escribir desde el archivo que oportunamente se identificó en una sentencia OPEN(). Este hecho adquiere una situación singular en los sistemas operativos UNIX (como el Linux) ya que todos los dispositivos de hardware se pueden ver como archivos de texto (en el directorio /dev). El software corriendo también se puede ver como un archivo de texto (directorio /proc) y por lo tanto pueden leerse abriéndolos como archivos con una sentencia OPEN(). Por lo tanto, un programa puede leer configuraciones y datos de la computadora donde está corriendo. Por lo tanto, se pueden acceder a todo un el conjunto de datos de la computadora como por ejemplo: la hora, fecha, la carga de trabajo de la CPU, incluso la temperatura de esta.
Puede no ponerse la palabra UNIT y se escribe directamente el número (siempre y cuando sea el primero número que aparece luego del paréntesis que abre el OPEN()), de lo contrario es UNIT=número.
FILE=’nombre del archivo’, indica el nombre del archivo al que ahora le asigno el número de UNIT. Puede ponerse una variable de caracteres que contenga el nombre del archivo. Pueden también incluirse los directorios con el fin de navegar por la computadora desde el root (/) donde comienza el sistema de directorios (que es una manera absoluta de navegar los directorios), o puede también navegarse en forma relativa a directorio donde se corre el programa, es decir puede poner ../../dir1/dir215 (es decir, subo 2 directorios y luego bajo al dir1 y dentro de este al dir2, ya que “../” significa subir un directorio).
ERR=’número’, indica el número de etiqueta de sentencia al que se salta si se produce algún error. Si se produce el error y el ERR no se programa (ya que es opcional, no obligatorio) el programa finaliza indicando que hubo error. En cambio, si la orden está, el programa continua en la sentencia a la que se etiquetó a saltar. Esta orden permite programar contingencias en casos de errores. Es muy útil para programas que corren largos períodos de tiempo sin control humano. Como ya indicamos ERR es opcional y puede no estar escrito en la sentencia.
IOSTAT=’variable entera’ indica una variable entera a la cual se le carga un número que es una referencia del error que apareció al intentar abrir un archivo. Este número figura en los manuales del compilador indicando la naturaleza el error. Si este valor es cero no hubo error alguno. Por ejemplo, no se puede abrir el archivo o el disco está lleno, etc. Es un complemento para funcionar en conjunto con el ERR, para que el propio programa resuelva la situación a través de alguna sección del código, programada para tal efecto.
Por ejemplo, si tengo un error, salto a una sección del programa que identifica el número en el IOSTAT que indica que el disco rígido está lleno y puedo hacer que mi programa borre archivos que ya no son necesarios. Entonces se lo hace volver a la operación OPEN() original (la que dio el error) pero ahora el programa puedo abrir el archivo sin error ya que el problema está resuelto. IOSTAT es opcional.
STATUS= es un parámetro, este puede ser: OLD, NEW, UNKNOWN o SCRATCH. Este parámetro sirve de control, si se indica OLD significa que el archivo tiene que estar en el directorio, si no se lo encuentra se declara error. En cambio si se indica NEW el archivo no debe estar en el directorio y el OPEN() lo creará en ese momento, si en cambio el archivo ya existía se declarará error. SCRATCH indica que el archivo es un borrador y será borrado cuando el programa finalice, o se ejecute la sentencia CLOSE() que cierre este OPEN(). UNKNOWN es el default, es decir, si no se escribe la orden STATUS, se considerará UNKNOWN. Este indica que da lo mismo que el archivo exista o no. Si no existe será creado cuando se quiera escribir, y si existe será leído o sobrescrito según lo que indique en el código. STATUS es opcional.
ACCESS se indica un parámetro que es ’SEQUENTIAL’ si el archivo es secuencial (que es el default, o sea que no es necesario ponerlo explícitamente), o si es de acceso directo cuyo parámetro es ’DIRECT’. ACCESS es opcional para archivos secuenciales y obligatorio para archivos de acceso directo.
RECL sólo se puede usar en combinación con ACCESS=’DIRECT’ e indica el tamaño de renglón para archivos de acceso directo. No se usa en caso de archivo secuencial.
Para indicar que un archivo dejará de usarse, en el uso común del
lenguaje “cerrarlo” , se utiliza la sentencia CLOSE() con parámetros
similares a las de OPEN().
Esta sentencia le da la orden al Sistema Operativo de que cierre la
conexión al archivo y que por consiguiente si estoy escribiendo en el
disco que guarde los datos (o si ya guardó parcialmente, que termine de
hacerlo). Si no está la orden el CLOSE() se hace automáticamente al
finalizar la ejecución del programa. En muchos sistemas, si por ejemplo,
se corta la electricidad antes de que esta orden se ejecute (el archivo
continua abierto) todos los datos ya escritos al disco rígido se
perderán. También es importante notar que en los OS modernos muchas
veces para evitar que se sature la conexión al disco, los datos pasan
por una cache en la memoria RAM donde esperan su turno para ser
guardados. Esta sentencia fuerza a que estos datos se salven el
disco.
Los parámetros de UNIT, ERR e IOSTAT son iguales a los descriptos para
la orden OPEN() y actúan de la misma manera. Mientras que los parámetros
de STATUS pueden ser ’KEEP’ (conservar) que es el default, y ’DELETE’
que borra el archivo al cerrarlo. ERR, IOSTAT y STATUS son
opcionales.
Para la lectura de datos se utiliza la sentencia READ() (leer en
inglés) o WRITE() (escribir en inglés). Estas órdenes en sus versiones
más simple, necesitan muy pocos parámetros. Hay que determinar de dónde
se lee o escribe, cómo se lo hace y que se lee o escribe. La sentencia
en su forma mínima podría escribirse así como ya hemos visto:
Pero hay muchos más parámetros que son de utilidad, en su versión más
extensa se puede escribir como:
Lista de variables
Lista de variables
Veamos que ordenan todos estos parámetros:
Unidad Lógica (UNIT) es el lugar asignado para leer o escribir un número. El UNIT es asignado por una sentencia OPEN() a un archivo en particular o por hardware/sofware a un dispositvo Puede ponerse el número sin la palabra UNIT y si hay un ’\(\divideontimes\)’ se está indicando que se lee del teclado o se escribe a la pantalla del que está corriendo el programa.
Formato, FMT= es el número de la etiqueta de la sentencia FORMAT que tiene la información de los formatos de esta entrada de datos. La palabra FMT= puede no estar, si este sigue después del Unidad Lógica. Si se pone un ’\(\divideontimes\)’ significa que se cede la soberanía de la decisión al Fortran, tanto para leer como para escribir.
END indica el número de etiqueta de sentencia a la que hay que saltar (como un GOTO) en caso de que se llegó al final del archivo que estoy leyendo16. END es opcional.
ERR, al igual que en la sentencia OPEN() este número es una etiqueta de sentencia al que se salta si se produce algún tipo de error. Si esta sentencia no se encuentra el programa finaliza indicando que hubo un error, si la sentencia está, el programa no termina y continua en la sentencia que tiene la etiqueta indicada. ERR es opcional.
IOSTAT, indica un número que identifica al error. Este se puede ir a buscar ya que está en los manuales del compilador, y obtener una descripción del problema. IOSTAT es opcional.
REC, es el número de renglón al cual voy a escribir o leer en el caso de archivos de acceso directo y es obligatorio para leste tipo de archivos. No tiene uso en el caso de archivos secuenciales.
La lista de variables se crea nombrando las variables separadas por
comas. Puede hacerse lo que se llama DO implícitos, por ejemplo:
o
Veamos un ejemplo interesante del uso del END para leer un archivo
secuencial en el cual no conozco cuantos renglones de datos posee. Esta
es una situación muy común en la vida real, sobre todo cuando los datos
viene de aparatos de medida automáticos que miden diferente cantidad de
datos dependiendo de condiciones externas como la meteorología:
Este programa lee con un READ() (en el cual está
indicado el END que apunta a la sentencia 99) valores
de dos vectores A y B. En cada lectura de los elementos de los vectores,
el programa incrementa el valor I y vuelve a leer los próximos datos, ya
que la sentencia GOTO 10 cierra el ciclo. Este ciclo
queda trabado leyendo ambos vectores hasta que se acaban los datos. En
el fin del archivo este ciclo se rompe, ya que el
READ() salta a la sentencia 99, tal como lo indica el
END.
Para saber cuántos valores se leyeron simplemente se le resta 1 a la
variable I y se lo asigna a N. De esta manera, quedan leídos los datos
del archivo en las variables A y B, y además en N queda guardado el
número de valores leídos del archivo. Este N lo puedo usar en sentencias
DOs posteriores para procesar ambos vectores.
En realidad la versión con menos parámetros posibles de escribir para
leer o escribir y que funcione sería así:
Lista de variables
Lista de variables
En esta versión del READ() o WRITE(),
no indico el formato que voy a usar y entonces se leen o se escriben los
datos en binario, tal como se encuentran en la memoria RAM de la
computadora: Con la ventaja de que ocupan mucho menos espacio, porque un
real*4 en binario, ocupa 4 bytes. En cambio si uso un formato y la
escribo en base 10 (formato humano) ocuparía 1 byte por dígito. Por otro
lado, la escritura o lectura es mucho más rápida porque no hay que
traducir de binario a decimal o a la inversa los datos que escribo o leo
al disco. Suelen ser muy útiles para transportar grandes cantidades de
datos ya que ocupan menos espacio y se pueden leer más rápido.
Como contra partida, debo leer los datos con una computadora similar a
la que usé para escribirlos ya que computadoras de distintos tipos
pueden no utilizar las mismas normas de definición de datos binarios, es
decir misma cantidad de bits en la mantisa y el exponente del número, o
distintos orden de los Byte para los números enteros.
Para el caso de los archivos de acceso directo defino en la sentencia
OPEN() la variable RECL= número que define el tamaño de
renglón, en el caso de los READ() o
WRITE() debo indicar que renglón leo y escribo. Para
ello se utiliza la variable REC que indica el número de renglón. Este
tipo de archivos se utiliza como base para construir el formato FITS
(Flexible Image Transport System) que se utiliza como estándar para
transferir y guardar datos astronómicos. Este estándar utiliza renglones
de 2880 Bytes de tamaño. Ejemplo:
En estas líneas, se leen las variables X,Y del renglón 128 sin tocar
ninguno de los renglones anteriores o posteriores del archivo. De la
misma manera se podría poner:
Donde ahora se escribiría en el renglón 99 sin modificar ninguno de los
otros renglones del archivo.
Hay varios comandos que sirven para manejar situaciones de la lectura de archivos secuenciales, veremos dos de los más útiles:
Donde UNIT, ERR y IOSTAT funcionan como ya hemos visto. UNIT, la unidad
lógica identifica el archivo a rebobinar. ERR y IOSTAT son opcionales y
pueden no estar.
Donde UNIT, ERR y IOSTAT cumplen con las mismas funciones, que
detallamos anteriormente. ERR y IOSTAT son opcionales.
En Fortran hay funciones preprogramadas (intrínsecas) que ya las hemos visto: raíz cuadrada, funciones trigonométricas, etc. Pero además de estas funciones se le permite al programador crear las suyas. Existen dos métodos para construir funciones en Fortran: a través de la Función Sentencia o de la Función Externa.
Es muy útil poder crear funciones, ahorra tiempo, hace los programas más compactos, enfocados y elegantes. Además permite que uno utilice funciones que ya se encuentran disponibles en libros o en páginas de internet. Sobre esto último, existen sitios web donde se discute cuál es el mejor algoritmo para una tarea determinada y cuales son sus mejores implementaciones en distintos lenguajes. Las funciones han tomado históricamente distintos nombres (procedimientos, subprogramas, etc) en distintos lenguajes de programación pero siempre existe una manera de definirlas.
Consiste en una sola sentencia aritmética definida en el programa.
Esta estructura existe en otros lenguajes, por ejemplo, en Python se la
llama función Lambda.
Se las define al comienzo del programa dándole un nombre a la función y
se las construye usando variables ficticias, es decir que no son las
variables del programa, sólo se las usa como referencia para construir
la fórmula matemática de la función y sólo valen en la sentencia. Es
decir, para indicar el orden y en que lugar se encuentran las distintas
variables de la fórmula a calcular.
La forma sería la siguiente:
función(var1,var,2,var3...) = expresión matemática usando las
variables var1, var2, var3,...
Donde función es el nombre que se le da a la función, las
var1,var2, var3, etc son las variables que se usan en la
expresión matemática. Estas variables indican el orden de los
argumentos con los que defino la función. Por eso su orden es muy
importante en el momento de llamarla.
Ejemplos:
Si se necesita una función discriminante (para ecuaciones cuadráticas),
la puedo construir de esta manera al comienzo del programa (donde defino
los tipos de variables del programa) escribiendo:
DISC(A,B,C) = B**2-4.*A*C
Entonces en el programa se puede escribir:
Program prueba_de_funcion_sentencia
DISC(A,B,C) = B**2-4.*A*C
\(\vdots\)
X= DISC(24.5, 34.5, 67.8) +25.4*C3+MAG
\(\vdots\)
MAGROJA = SQRT(DISC(z1+3, 45.5*8, (z2+z4+f6)+28)
\(\vdots\)
Detalles a tener en cuenta:
Las variables (var1,var2,...) pueden ser de cualquier tipo incluyendo variables lógicas o de caracteres.
Las funciones para el programa son variables, es decir la función es una variable que cuando se llama realiza un cálculo y entrega el resultado de su ejecución, en vez de ir a buscar un número que este guardado en la memoria. Por lo tanto una función, ya que es una variable, puede ser integer, real*4, real*8, complex, character o logical, etc.
De los cursos de análisis matemático uno adquiere la idea de que la
única manera de resolver los problemas pasa por obtener siempre su
solución analítica. Pero en la vida real, esa situación es más bien
rara, o imposible. Incluyendo el hecho que en el caso particular de una
integral puede que esta no tenga primitiva o que sea muy complejo o
laborioso encontrarla. Más aún si lo que se lo quiere resolver es una
ecuación diferencial. Por esta razón, en problemas muy complejos se usan
los sistemas de computación con el fin aproximar la solución, es decir
obtener una solución numérica. Esta puede ser en algunos casos una
solución exactas o a veces aproximada. Desarrollaremos un caso en
particular como ejemplo.
Uno de los métodos más simples de aproximar numéricamente el resultado
de una integral definida es el método de los trapecios. Vamos a ver con
un ejemplo cómo funciona este método desde el punto de vista
computacional. Un tratamiento más profundo de sus propiedades incluyendo
ventajas y desventajas se estudia en cursos de análisis numérico.
Con este método lo que se desea es integrar la función \(f(x)\) en el intervalo \([a,b]\), es decir queremos medir el área
bajo la curva. Para ello dividiremos el intervalo en varios
subintervalos más pequeños y veremos cómo se podría aproximar con un
trapecio al área bajo la curva de la función \(f(x)\). Ya que la idea del método es
dividir el área en \(n\) subintervalos
de tamaño h, por lo que \(h =
(b-a)/n\). Si llamo \(x_i\) a
los puntos que separan cada uno de estos subintervalos tendríamos
que:
\(a=x_0\), \(x_i=x_0+ih\) y \(b= x_n\)
En la figura 10.1 veamos cómo sería esta situación
con un dibujo de la función \(f(x)\)
entre los límites \(x_i\) y \(x_{i+1}\), (donde \(x_{i+1} = x_i + h\)).
:
Entonces, el área para el trapecio del la figura es:
\[A_i = h f(x_i) + \frac{h}{2} [f(x_{i+1})
- f(x_i)] = \frac{h}{2} [f(x_{i+1}) + f(x_i)]\]
y la aproximación a la integral será la suma de todos los trapecios
\(A_i\)
\[Integral = \sum_{i=0}^{n}{
A_i}\]
si hago todos lo reemplazos, obtengo:17
\[Integral = \frac{h}{2}[ f(a)+f(b)] +
h \sum_{i=1}^{n-1}f(x_i)\]
Veamos el programa que haría este cálculo y tomemos con función \(f(x)=x^2\)
y la integraremos en el intervalo [0,1]
En forma teórica:
\[\int_{0}^{1} x^2 dx = 1/3\]
Veamos como sería un programa y la precisión de los resultados.
\(\ \ \ \ \ \ \ \) program
x2
\(\ \ \ \ \ \ \ \) real*8 integral
\(\ \ \ \ \ \ \ \) f(z)=z*z
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \) x0=0.
\(\ \ \ \ \ \ \ \) xn=1.
\(\ \ \ \ \ \ \ \) read(*,*)n
\(\ \ \ \ \ \ \ \) h=(xn-x0)/n
\(\ \ \ \ \ \ \ \) integral=0.
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \) do i=1,n-1
\(\ \ \ \ \ \ \ \ \ \ \ \) x=i*h
\(\ \ \ \ \ \ \ \ \ \ \ \) integral=integral+f(x)
\(\ \ \ \ \ \ \ \) enddo
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \) integral=integral*h+(f(xn)+f(x0))*h/2
\(\ \ \ \ \ \ \ \) write(*,*)’Para ’, n,’ intervalos, la integral es=’,integral
\(\ \ \ \ \ \ \ \)
end
Si corro este programa para distintos valores de la cantidad de
intervalos, obtengo los resultados del tabla 10.1.
Como puede verse en la tabla no sirve pensar que se puede llegar al
límite infinito sumando una cantidad gigantesca de trapecios debido a
los errores de redondeo. Un buen resultado se obtiene cerca del
1,000,000 de trapecios, tomando intervalos más pequeños el resultado se
deteriora. Pero por otro lado, la tabla nos muestra que según lo que se
requiera de precisión en el resultado hay formas de evaluar este
problema, y además de encontrar y determinar un resultado aproximado muy
bueno incluyendo alguna idea de la precisión. En este caso hemos
obtenido la integral con un error \(10^{-7}\).
En este programa usamos \(f(x)=x^2\)
como función a integrar. Si quisiera integrar otra función en otro rango
de valores, sólo tendría que cambiar la definición de la función por
otra y modificar los límites del intervalo a integrar. El programa no
requiere ninguna otra modificación. Sólo hay quecambiar la función y
volver a compilarlo.
| Cantidad de intervalos | Resultado de la aproximación |
| de la integral | |
| 10 | 0.33500001696869747 |
| 100 | 0.33334997741140865 |
| 1,000 | 0.33333354714617608 |
| 10,000 | 0.33333330969899705 |
| 100,000 | 0.33333330800677946 |
| 1,000,000 | 0.33333333080419814 |
| 10,000,000 | 0.33333334502431866 |
| 100,000,000 | 0.33333332725965703 |
| 1,000,000,000 | 0.33333330505514902 |
El método de trapecios, no es el método más usado pero si es un método que tiene interés académico porque sirve para entender la complejidad del cálculo y determinar cotas teóricas al problema de aproximar la integral. Existen métodos muchos mejores que el de trapecios y modificaciones para hacerlo mucho más eficiente.
La función sentencia que vimos en la sección anterior es muy útil
pero tiene sus limitaciones. La mayor de ellas es que sólo permite una
fórmula matemática que se escriba en un solo renglón. Por ejemplo, una
función a trozos no se podría programar como función sentencia, ya que
se necesitarían al menos más de un renglón para programarla con el
comando IF().
En cambio, la función externa, trabaja como si fuera otro programa y
este es llamado por el programa principal al igual que la función
sentencia. Un esquema simple, sería:
\(\ \ \ \ \ \ \ \)program
Principal
\(\ \ \ \ \ \ \ \)real*4 F
\(\ \ \ \ \ \ \ \vdots\)
\(\ \ \ \ \ \ \ \)A= F(x)+5.0
\(\ \ \ \ \ \ \ \vdots\)
\(\ \ \ \ \ \ \ \)END
\(\ \ \ \ \ \ \ \)Function F(x)
\(\ \ \ \ \ \ \ \vdots\)
\(\ \ \ \ \ \ \ \)F = \(\cdots\)
\(\ \ \ \ \ \ \ \)RETURN
\(\ \ \ \ \ \ \
\)END
Como se ve en el esquema, la función fue escrita en el mismo archivo del
programa, después de la sentencia END18.
Notar que en general la función tiene la misma estructura que un
programa salvo por el inicio como FUNCTION nombre(variables que
recibe) y la orden RETURN que devuelve la
ejecución hacia el programa principal.
Detalles que definen a la función externa:
Puede haber muchas funciones que son utilizadas por un programa.
Las funciones tienen variables internas que guardan datos que son de la función, cualquier modificación que se realice sobre ellas no afecta las variables del programa principal aunque tengan el mismo nombre), con la excepción del nombre de la función que retorna con el valor del resultado al programa principal).
La orden RETURN devuelve la ejecución al lugar exacto donde la función fue llamada. Un programa puede llamar repetidamente a la función desde distintos lugares.
Las funciones externas, al igual que la función sentencia son para el programa principal variables y cumplen con las reglas de estas. Según la primera letra de su nombre serán enteras o reales y se deberá definir cualquier otro tipo en forma explícita. Ejemplo: Si escribo Complex G(x,y) en el programa principal, en el comienzo de la función se deberá también escribir Complex Function G(x,y), para definirla como compleja.
La función cuando es llamada depende para realizar su cálculo de
las variables de referencia que se encuentran dentro del paréntesis. A
estas variables se las denomina argumentos de la función. Los nombres de
estos argumentos en el programa que llama a la función, pueden o no
coincidir con los que se usan en la función para hacer los cálculos. Es
decir, pueden tener otros nombres, ya que en realidad se copian en el
momento de la llamada a la función. Pero tienen que ser del mismo tipo
de variable. Si el primer argumento es un entero, también debe ser un
entero en la función, lo mismo para el segundo o tercero y así. Incluso
pueden ser variables dimensionadas y en ese caso no sólo debe coincidir
el tipo de variable sino la dimensión y debe repetirse la definición de
dimensión en la función. Ejemplo:
\(\ \ \ \ \ \ \ \)programa
principal
\(\ \ \ \ \ \ \ \)REAL*4 A(100)
\(\ \ \ \ \ \ \ \)Complex C
\(\ \ \ \ \ \ \ \vdots\)
\(\ \ \ \ \ \ \ \)Z = F(A,C)
\(\ \ \ \ \ \ \ \vdots\)
\(\ \ \ \ \ \ \ \)END
\(\ \ \ \ \ \ \ \)Function F(X2,B)
\(\ \ \ \ \ \ \ \)REAL*4 X2(100)
\(\ \ \ \ \ \ \ \)COMPLEX B
\(\ \ \ \ \ \ \ \vdots\)
\(\ \ \ \ \ \ \ \)RETURN
\(\ \ \ \ \ \ \
\)END
En este ejemplo, la función fue escrita de argumentos X2 y B, pero en el
programa principal se la llama con las variables A y C. Donde A es
vector de 100 elementos y C es un número complejo. Por eso X2 y B son
definidas en la función del mismo tipo que las variables del programa
principal. Note que el orden es quien decide cuál variable se copia a la
correcta, en este caso la primera es el vector y la segunda es el
complejo. El orden en el llamado determina cuál variable es cuál en la
función.
Las funciones fueron inventadas para el Fortran y copiadas con modificaciones en todos los lenguajes más modernos. Se las suele llamar en distintas encarnaciones como procedimientos, subprogramas, etc. En el caso de Python, que veremos más adelante en la cursada, se viola la idea de función matemática ya que estas pueden devolver mas de un valor. Pero en sí, son muy similares a las de Fortran.
Por ejemplo, si programamos una función que nos calcule la serie
\(\sum_{i=1}^n{1/i^k}\), donde
básicamente le enviamos N, K y nos devuelve la suma de la serie, sería
así:
\(\ \ \ \ \ \ \ \) Function
Serie(n,k)
\(\ \ \ \ \ \ \ \)
Serie=0.
\(\ \ \ \ \ \ \ \) DO i=1, n
\(\ \ \ \ \ \ \ \ \ \ \) x = i
\(\ \ \ \ \ \ \ \ \ \ \) Serie = Serie + 1/ x**k
\(\ \ \ \ \ \ \ \)
ENDDO
\(\ \ \ \ \ \ \ \)
RETURN
\(\ \ \ \ \ \ \ \)
end
En muchos programas, en particular en algunos muy largos y complejos
donde varias veces se rehacen los mismos cálculos una y otra vez podrían
utilizarse funciones externas para simplificar el código y volverlo más
simple y compacto ¿Pero qué pasa si lo que se quiere calcular no tiene
estructura de función? Esto pasaría cuando tengo un problema a resolver
donde la solución no es un sólo resultado, sino que la solución serían
varios valores (por ejemplo coordenadas y velocidades), por lo cual una
función no me serviría. Resumiendo, necesito un subprograma parecido la
función externa, pero que a diferencia de la función me devuelva varios
resultados.
Para este tipo de trabajo se diseñaron las Subrutinas,
que tienen las siguientes propiedades y formas de uso:
Se escriben en forma externa al programa, tal como vimos lo hacen las funciones externas.
Intercambian con el programa principal una lista de variables. A esas variables se las llama argumentos (como en la función).
Los argumentos son variables que se envían del programa a la subrutina y cuando esta termina son devueltos. Sólo esa lista es intercambiada. No se define cuales de estos argumentos son datos que ingresan información o cuales son los que devuelven los resultados19. Es decir, los argumentos son una lista de variables que se intercambia con la subrutina, donde cualquiera de estas variables puede ser modificada o no.
Las subrutinas son llamadas del programa principal a partir de la orden CALL Nombre de la subroutina(lista de variables). No son parte de un cálculo o una asignación, como las funciones.
Las subrutinas se escriben al final de programa principal en el mismo archivo o en archivos separados que se compilan junto al principal. Se debe indicar como primer sentencia la orden: SUBROUTINE Nombre de la subrutina(lista de variables).
Los argumentos se copian a variables en el espacio de memoria asignado a la subrutina y cuando esta termina se copian de nuevo a la memoria del programa. Las variables internas de la subrutina desaparecen en el momento que esta termina (veremos en este capítulo una forma de evitar esto).
Al igual que en las funciones externas, es necesario que las variables en los argumentos de llamada de la subrutina sean del mismo tipo y dimensión en el programa y en la subrutina. Por eso, el orden de cada variable en los argumentos debe ser el mismo en el programa principal y en la subrutina.
La subrutina retorna al programa cuando ejecuta la sentencia RETURN. Este retorno se hace exactamente al lugar donde fue llamada. Un programa puede llamar a una subrutina todas las veces que sea necesario.
La última sentencia de una subrutina es al igual que cualquier otro programa, es la orden END.
Una subrutina puede llamar a otra subrutina y cuando termina devuelve el control a la que la llamó en el punto que la llamó.
Una subrutina puede llamarse a sí misma. Esta propiedad se llama recursividad y discutiremos el funcionamiento de esta propiedad con detalle más adelante.
Si en el programa existe una llamada a una subrutina en particular pero esta no es encontrada por el compilador se señalará como error. No se indica como error la existencia de una subrutina que no es usada por el programa principal u otras subrutinas.
Las subrutinas pueden no estar escritas en el mismo lenguaje que el programa que las llama, pero sí se deberán respetar el tipo de variable, su dimensión y el orden de los argumentos en la llamada.
Las subrutinas pueden precompilarse en grupos y estos archivos se los denomina bibliotecas. Los sistemas operativos tienen muchas bibliotecas que son accesibles desde los programas, incluso algunas de estas, las consideradas esenciales están cargadas en la memoria ram. Por ejemplo, existen bibliotecas para que los programas Fortran puedan hacer dibujos (PGPLOT, etc) o hacer cálculos vectoriales (BLAS, etc).
Veamos como funciona en un caso real, donde el programa Prueba llama
a la subrutina TEST
\(\ \ \ \ \ \ \ \) Program
Prueba
\(\ \ \ \ \ \ \ \) REAL*4 C(100)
\(\ \ \ \ \ \ \ \) Integer B
\(\ \ \ \ \ \ \ \) \(\vdots\)
\(\ \ \ \ \ \ \ \) CALL TEST(A, B, C)
\(\ \ \ \ \ \ \ \) \(\vdots\)
\(\ \ \ \ \ \ \ \)
END
\(\ \ \ \ \ \ \ \) SUBROUTINE
TEST(X,Y,Z)
\(\ \ \ \ \ \ \ \) REAL*4 Z(100)
\(\ \ \ \ \ \ \ \) Integer Y
\(\ \ \ \ \ \ \ \) \(\vdots\)
\(\ \ \ \ \ \ \ \) RETURN
\(\ \ \ \ \ \ \ \)
END
En la figura 11.1 podemos ver un esquema de como
las variables son transferidas del programa principal a la subrutina,
para el caso del ejemplo que acabamos de ver. Notar que sólo A, B y C
que son los argumentos de la llamada a la subrutina en el programa
Prueba y son las únicas variables que son copiadas a la subrutina. Otras
variables del programa como D, E y X no son transferidas y su existencia
será desconocida por la subrutina. Las variables A, B y C son
transferidas a un nuevo espacio de memoria como las variables X, Y y Z.
Como B es una variable entera, sólo puede ser transferida a otra
variable entera, por eso Y es definida como entera también en la
subrutina. Y en el caso del vector C de 100 elementos tiene que ser
recibida por una variable de igual dimensión y tipo, en este caso Z que
fue definida correctamente para el caso en la subrutina Test. Note que
el orden en los argumentos en el programa principal es concordante con
la variable elegida en la subrutina (de igual tipo y
dimensionalidad).
Cuando una subrutina se encuentra con la sentencia RETURN termina su
trabajo y retorna las variables que están en los argumentos al programa
principal, volviendo a reasignar los valores. En este caso las variables
X, Y y Z se copian a A, B, y C. Las variables G y E de la subrutina test
se pierden cuando esta termina y se las considera variables temporales20. En cambio en el programa Prueba
las variables D, E y X nunca se enteraron de la llamada a Test, a pesar
de que en la subrutina había dos variables con igual nombre (X y E).
Si, en cambio, es posible hacer lo siguiente:
\(\ \ \ \ \ \ \ \) CALL
TEST(A+2.5, B, C)
En este ejemplo, se hace la cuenta A+2.5 y el resultado se envía a la
subrutina y es asignado a la variable X. Pero en este caso en particular
inhibimos a la variable A de recibir cualquier resultado de producto de
la ejecución de la subrutina.
Resumiendo, la subrutina cuando se ejecuta crea su propio universo de
variables y sólo recibe datos por los argumentos de la llamada. Este
universo de variables desaparece cuando la subrutina termina. Si la
subrutina es vuelta a llamar el espacio de memoria se crea nuevamente,
pero los datos en las variables anteriores no se conservan.
Como ejemplos realizaremos dos subrutinas que se encarguen de la transformación de coordenadas polares a cartesianas y viceversa, junto con un programa que las llama y realiza ambas transformaciones.
\(\ \ \ \ \ \ \ \)program polares
\(\ \ \ \ \ \ \ \)pi=atan(1)*4
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)write(*,*)’Ingrese X,Y’
\(\ \ \ \ \ \ \ \)read(*,*) X,Y
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)call pola(X,Y,r,theta)
\(\ \ \ \ \ \ \ \)write(*,*)’R =’,r,’Theta =’, theta/pi*180
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)call cartesianas(X,Y,r,theta)
\(\ \ \ \ \ \ \ \)write(*,*)’x =’,X,’y =’,Y
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)end
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)Subroutine pola(x,y,r,theta)
\(\ \ \ \ \ \ \ \)r = sqrt(x*x + y*y)
\(\ \ \ \ \ \ \ \)theta = atan2(y,x)
\(\ \ \ \ \ \ \ \)return
\(\ \ \ \ \ \ \ \)end
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)Subroutine cartesianas(x,y,r,theta)
\(\ \ \ \ \ \ \ \)x=r*cos(theta)
\(\ \ \ \ \ \ \ \)y=r*sin(theta)
\(\ \ \ \ \ \ \ \)return
\(\ \ \ \ \ \ \ \)end
Las subrutinas traen aparejado muchas mejoras para resolver problemas complejos que suelen generar programas grandes y largos. Esto se debe a que permiten dividir el problema grande en muchos pequeños cuyo solución es más fácil de manejar y testear. Existen libros21 y muchas páginas web con subrutinas ya programadas que abarcan casi todas las áreas de la matemática. Esto no sólo es cierto para algoritmos matemáticos simples, sino que también para los muy complejos. Desarrollar algoritmos para computadoras es toda una rama de la matemática contemporánea. El uso masivo de computadoras creó a su vez otros campos en el desarrollo de la matemática. En capítulos siguientes trataremos con ejemplo dos de estos campos, el de ordenar y el de generar modelos con números al azar.
¿Cuáles son las metas de estas nuevas áreas de la matemática asociada
a la computación? En si, resolver los problemas con algoritmos novedosos
o variantes que tengan las siguientes propiedades:
Que realicen la menor cantidad de operaciones matemáticas. En si, menos operaciones implica menos tiempo de computación para resolver el problema y por lo tanto mayor eficiencia en su uso. También menos pérdida de precisión en los resultados.
Establecer cuál es el número de estas operaciones para comparar con otros algoritmos.
Establecer cómo la cantidad de operaciones crece cuando aumenta el tamaño del problema (ejemplo: Si mi problema tiene un orden de tamaño N ¿El tiempo que tarda va con N elevado alguna potencia?
Si no es posible calcular la cantidad de operaciones ¿Es posible obtener un número promedio de estas?
¿Cuál es la precisión matemática del resultado? ¿Hasta qué punto puede crecer el problema y se obtendría una solución útil?
Por otro lado, hay otra serie de ventajas de usar en forma masiva subrutinas para resolver un problema, que también son dignas de mención:
Permiten trabajar en colaboración con otros colegas sobre un mismo proyecto, ya que el trabajo puede dividirse en partes.
Escribir utilizando subrutinas hace que se puede recuperar muy fácilmente el trabajo de otros proyectos anteriores ya terminados, en los cuales se han implementado algoritmos para realizar ciertos cálculos que ahora se tendrán que volver a hacer.
Permiten llegado el caso de encontrar un algoritmo más eficiente, mejorar un programa con solo modificar la subrutina que lo controla.
Con el uso de subrutinas para todos los algoritmos necesarios se reduce el programa principal a que este sea el que llama en orden a las subrutinas y en si, son las subrutinas que realizan el trabajo, donde cada una lo hace parcialmente, pero el conjunto de todas lo resuelve.
Las funciones pueden definirse como external
haciendo:
External nombre_de_la_función
Esta orden tiene dos formas de trabajo muy diferentes. La primera de
ellas es la de reemplazar una función intrínseca como por ejemplo puede
ser el cos(), por una creada por el propio usuario. Es decir, si se
trabaja en una computadora cuyo compilador Fortran no tiene una función
cos() que satisfaga los requerimientos necesarios (por ejemplo:
precisión en los decimales). Esta puede ser reemplazada por una propia,
programada por el usuario. Con poner la orden, tal como está en el
ejemplo, ya no se llama a la función intrínseca sino a la construida por
el usuario. Se podría evitar hacer esto, por ejemplo, poniéndolo otro
nombre, como COS_mio() pero había que editar todo el programa para
buscar las llamadas de cos() y reemplazarlas por COS_mio(). En cambio,
de esta manera, con EXTERNAL, no hay que hacer ningún reemplazo. El
usuario es ahora el dueño del nombre cos() para su función.
La otra función de la orden EXTERNAL es declarar que una función puede
ser parte de los argumentos en el llamado de una subrutina, y por lo
tanto la subrutina queda habilitada para usar la función al recibirla en
los argumentos como una variable mas.
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)PROGRAM AREA
\(\ \ \ \ \ \ \ \)EXTERNAL FUN
\(\ \ \ \ \ \ \ \)\(\vdots\)
\(\ \ \ \ \ \ \ \)CALL RUNGE (FUN, LOW, HIGH, AREA2 )
\(\ \ \ \ \ \ \ \)\(\vdots\)
\(\ \ \ \ \ \ \ \)END
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)FUNCTION FUN( X )
\(\ \ \ \ \ \ \ \)\(\vdots\)
\(\ \ \ \ \ \ \ \)RETURN
\(\ \ \ \ \ \ \ \)END
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)SUBROUTINE RUNGE ( F, X0, X1, A )
\(\ \ \ \ \ \ \ \)\(\vdots\)
\(\ \ \ \ \ \ \ \)RETURN
\(\ \ \ \ \ \ \ \)END
Hasta ahora hemos visto que la única forma de transferir datos entre un programa y una subrutina es a través de los argumentos que se encuentra en la llamada a la subrutina. Pero forma tiene una limitación a pocas variables, y por ello no es el único método. Cuando las variables en los argumentos es muy grande se prefiere enviarlos a través de la sentencia COMMON usada en combinación con la orden INCLUDE.
Para utilizar este comando en la zona de definición de variables debo
indicar el COMMON que defino con su nombre22 y
sus variables asociadas. La forma general de la definición sería:
\(\ \ \ \ \ \ \ \) COMMON
/NOMBRE1/ Lista de variables
\(\ \ \ \ \ \ \ \) COMMON
/NOMBRE2/ Lista de variables
Ejemplo:
\(\ \ \ \ \ \ \ \) COMMON
/listado1/ A,B,C,IK,X(1000)
\(\ \ \ \ \ \ \ \) COMMON
/listado2/ B1,B2,B3,B4
y en las subrutinas tendría poner:
\(\ \ \ \ \ \ \ \) SUBROUTINE
SUB1()
\(\ \ \ \ \ \ \ \) COMMON /listado1/ X,Y,Z,J,ES(1000)
\(\ \ \ \ \ \ \ \) \(\vdots\)
\(\ \ \ \ \ \ \ \) RETURN
\(\ \ \ \ \ \ \ \)
END
Vemos que esta subrutina recibe también como argumentos las variables
del COMMON listado1
Pero la segunda podría ser asi:
\(\ \ \ \ \ \ \ \) SUBROUTINE
SUB2()
\(\ \ \ \ \ \ \ \) COMMON /listado1/ X,Y,Z,J,ES(1000)
\(\ \ \ \ \ \ \ \) COMMON /listado2/ B1,B2,B3,B4
\(\ \ \ \ \ \ \ \) \(\vdots\)
\(\ \ \ \ \ \ \ \) RETURN
\(\ \ \ \ \ \ \ \)
END
Es decir la SUB1 recibe los argumentos del primer COMMON, mientras la
segunda SUB2 recibe los argumentos de ambos COMMONs: listado1 y
listado2. Una tercera subrutina podría no recibir ninguno de los dos
listados de variables, es decir, no tendría ninguna de las sentencias
COMMON en su código.
La sentencia INCLUDE “nombre_de_un_archivo" hace que el compilador
cargue y compile la secuencia de Fortran que está escrita en el archivo
nombrado, en ese lugar del programa. Es una práctica común poner muchas
de las definiciones de variables y COMMON´s en un archivo aparte y que
este sea incluido por el compilador, tanto en el programa principal,
como en las subrutinas. Esto permite que no haya diferencias entre las
definiciones de las variables que se comparten como argumentos entre el
programa principal y sus subprogramas. Los archivos que tienen esta
información (y que va a ser incluida) suelen tener terminación “.h” como
norma.
Se denomina recursión cuando una subrutina se llama
a si misma. Esto tiene sentido cuando un problema es posible reducirlo
en un orden de complejidad pero sigue siendo el mismo problema. Esta
situación se da en algoritmos tipo diagrama de árbol, que son muy
usados, por ejemplo, en programas de cálculo de la evolución dinámica de
las estrellas en una galaxia.
Para ver un ejemplo real y simple estudiaremos el factorial, que cumple
con las propiedades que hemos descripto. Recordar que factorial de N, se
puede escribir como N!=N(N-1)!. Es decir convierto el factorial de N en
resolver ahora el factorial de (N-1)!. Y entonces podría repetir el
procedimiento hasta que mi problema quede reducido al factorial de 1 que
por definición 1!=1.
Por otro lado hay que recordar que cuando una subrutina es llamada, crea
su propio universo de variables que no son ni las del programa
principal, ni el de las otras subrutinas. Incluso, cuando una subrutina
se llama así misma crea otra zona memoria para sus variables, que no se
comparte contra su propia versión iniclal. Es decir la subrutina madre
no comparte variables con ls subrutina hija, salvo las que se reasignan
porque están en los argumentos del llamado.
Podemos entonces hacer un programa muy compacto que resuelva el
factorial usando una subrutina recursiva y sería así:
\(\ \ \ \ \ \ \ \) program
factor
\(\ \ \ \ \ \ \ \) write(*,*)’Cual es el numero:’
\(\ \ \ \ \ \ \ \) read(*,*) n
\(\ \ \ \ \ \ \ \) call factorial(n,p)
\(\ \ \ \ \ \ \ \) write(*,*) p
\(\ \ \ \ \ \ \ \)
end
\(\ \ \ \ \ \ \ \) Recursive
Subroutine factorial(n,p)
\(\ \ \ \ \ \ \ \) if(n.gt.1) then
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \) call factorial(n-1,p)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \) p=p*n
\(\ \ \ \ \ \ \ \) else
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \) p=1
\(\ \ \ \ \ \ \ \) endif
\(\ \ \ \ \ \ \ \) return
\(\ \ \ \ \ \ \ \)
end
En este caso en particular para el compilador GFORTRAN debo indicar que
la subrutina es recursiva con el aviso de RECURSIVE en el nombre de la
subrutina, pero esto puede cambiar según el compilador Fortran que se
use.
La función SAVE se usa en la subrutinas de la siguiente manera:
\(\ \ \ \ \ \ \ \) SAVE lista
de variables
Esta sentencia se agrega al principio de la subrutina e indica cuales
variables se conserven cuando la subrutina se cierra y los valores
guardados sirven para ser usados en el próximo llamado. Esto destruye el
modelo del uso de memoria que hemos descriptos (es una forma antigua de
programar en Fortran) y su uso inhibe la posibilidad de hacer
recursiones. Esta sentencia vuelve a un uso de memoria más antiguo donde
la subrutinas podían volver llamarse y las variables conservaban los
valores de la llamada anterior.
Veremos en esta sección algunas subrutinas y sus algoritmos que tienen especial interés, por su uso cotidiano en las áreas de investigación o por el tema particular en el que se las utiliza.
La generación de números al azar es muy útil en muchos campos de la
ciencia, pero su uso supera al tema científico. Por ejemplo: dados,
mazos de cartas, ruletas, ruedas de la fortuna con premios anotados,
bolilleros para los sorteos de los temas de concursos, sorteos con
papelitos en una bolsa, sistemas de lotería estatales. Todos estos no
son más que ingenios mecánicos para generar un resultado que se supone
que es por azar. Por otro lado, los juegos del celular o de la
Playstation tienen que generar un sistema de azar para que el monstruo
que nos persigue cuando jugamos no repita el mismo esquema una y otra
vez, y el juego no termine resultando aburrido y tedioso.
A los números al azar se los suele denominar como números random o
aleatorios. Se pueden construir generadores de números al azar
utilizando computadoras, pero estos no generan secuencias infinitas,
sólo una secuencia inicial finita de números es estadísticamente
azarosa. Aunque esta secuencia pueden ser muy larga, se llega a un punto
en que los números se repiten y la secuencia deja de ser formada con
valores al azar. Esta área es un tema de investigación actual y existen
muchos algoritmos muy diferentes para realizar esta tarea. Por lo cual
esta explicación debe ser tomada como una introducción muy simple al
área. Pero sirve orientar en la complejidad y usos de estos
números.
En ciencia se usan mucho estos algoritmos para realizar simulaciones de
procesos físicos. Por ejemplo, simular observaciones con sus errores
para luego aplicarle los procesos de reducción y análisis de datos, con
el fin de comparar los resultados con los datos originales, entre muchos
otros usos. Otro ejemplo, es el de calcular las probabilidades de
observación de un fenómeno físico desde cierta perspectiva en
particular. A este último tipo de cálculo se lo llama método de Monte
Carlo. A los modelos realizados con estos números al azar se los suele
llamar “realizaciones”.
Veamos un método para generar una secuencia de números al azar, este
algoritmo venía programado en varias generaciones de calculadoras de la
empresa Texas Instruments. Pero primero recordamos que el resto de una
división se lo suele llamar módulo, es decir el resto de A divido B,
seria el \(A\ mod(B)\). El módulo
existe en Fortran como función intrínseca y suele utilizarse en los
generadores de números al azar. Estos generadores dan un secuencia de
números que los denominaremos: \(X_0\),\(X_1\), \(X_3\),...,\(X_N\) y para generarlos usamos el siguiente
algoritmo:
\[X_{i+1} = \frac{(A X_i +
C)mod(M)}{M}\]
Es decir, con el valor al azar \(X_i\)
construimos el número al azar que sigue \(X_{i+1}\). Al primer \(X\) de la secuencia (el \(X_0\)) hay que asignarlo, es decir no
proviene del algoritmo y con él se inicia la secuencia. A este primer
número se lo llama la semilla. Muchas veces se prefiere que la semilla
sea fija, para que se repita la secuencia igual, pero si lo que importa
es que la secuencia sea siempre diferente (como en un juego) se cambia
la semilla en cada comienzo de la simulación, para que cada corrida del
programa se realice con diferentes números. En los juegos muchas veces
se usa el reloj de la computadora (recordar que el celular, como la
Nintendo o la Playstation son computadoras y tienen un reloj interno)
para tomar el tiempo con muchos decimales y con el fin de usarlo como la
semilla que inicia una nueva secuencia.
Note que con este algoritmo hacemos una cuenta y a ese resultado le
tomamos el mod(M) o sea nos quedamos con el resto de la división por M.
El resto no puede ser mayor que el divisor (M) y si después lo dividimos
por M, nos quedan números en el intervalo \([0,1)\). Por lo tanto, nuestra secuencia de
números al azar está siempre en ese intervalo.
En este algoritmo A, C y M tienen números prefijados que se conocen por dar secuencias bastante largas. La razón de que las secuencias de números al azar se agoten se debe principalmente a la pérdida de decimales por el redondeo en las operaciones de punto flotante.
La subrutina sería así:
\(\ \ \ \ \ \ \ \) Subroutine
azar(X)
\(\ \ \ \ \ \ \ \) real*8 X
\(\ \ \ \ \ \ \ \) integer A,C
\(\ \ \ \ \ \ \ \) A = 24298
\(\ \ \ \ \ \ \ \) C = 99991
\(\ \ \ \ \ \ \ \) M = 199017
\(\ \ \ \ \ \ \ \) X = MOD(X * A + C,M) /M
\(\ \ \ \ \ \ \ \) return
\(\ \ \ \ \ \ \ \)
end
Esta rutina nos dará números al azar con una distribución uniforme, es
decir, cualquier número tiene la misma probabilidad de aparecer que
otro. Existen algoritmos para otras distribuciones, como por ejemplo,
una campana de Gauss, etc, donde ahora algunos números son más probables
que otros. Si se quisiera que los números estén en algún otro intervalo
como en una ruleta, siempre se puede hacer un cambio de escala lineal
para moverlos sin que estos cambien sus propiedades. Es decir, estoy en
el intervalo \([0,1)\) y quiero pasar
al intervalo \([A,B)\) simplemente
calculo mi nueva secuencia haciendo \(X^* = X
* (B - A) + A\). Por ejemplo, si quisiera imitar una ruleta mi
nueva secuencia tendría que estar en el intervalo \([0,37)\). Por lo tanto, la secuencia que
imitaría a la ruleta sería \(X^* = X * 37
+ 0\). Y consideraría que el valor entero de \(X^*\) es el valor que sale de cada jugada
de la ruleta virtual.
Con la subrutina que genera números al azar, veremos una manera de calcular el número \(\pi\). Pero primero repasaremos en modo sucinto algunos conceptos de teoría de probabilidades. Se denomina frecuencia a la cantidad de veces de que un cierto estado se repita en un experimento frente a todos los experimentos que se han realizado. La frecuencia es algo que se puede medir. Por ejemplo, tirando una moneda y contando la cantidad de veces que sale cara frente a las veces que esa moneda fue arrojada.
La probabilidad de que ese estado en particular suceda es un
resultado teórico que se obtendría de repetir infinitamente el
experimento. La frecuencia entonces se convierte en probabilidad cuando
el número de experimentos tiende a infinito. En este caso vamos a asumir
que cuando repito mucho veces un experimento y mido la frecuencia se
parecerá bastante a la probabilidad. Es decir, puedo tirar una moneda
muchas veces al aire, y medir la frecuencia de que salga cara y no seca.
Pero sólo cuando se la tire infinitas veces obtendré la probabilidad del
suceso.
Pero como la probabilidad es una definición: prob= casos
favorables/casos totales, para una moneda perfecta tengo: una cara/dos
posibilidades (cara mas seca). O sea que la probabilidad de obtener cara
es \(Prob= 0.50\).
Con esta explicación vamos a calcular la probabilidad de un
experimento curioso, que es el siguiente:
Tengo un cuadrado perfecto dibujado en el piso y le arrojo piedras. Si una piedra cae afuera la vuelvo a tirar.
Tengo un contador que lleva la cuenta de todas las piedras que se arrojan.
Dentro de ese cuadro dibujo un círculo centrado y con el radio tal de que es tangente a todos los lados de cuadrado. Ver dibujo 12.1 .
Llevo la cuenta de todas piedras que caen en el círculo.
Realizo este experimento utilizando la computadora. La posición de la piedra la determino generando dos números al azar con distribución uniforme. Es decir la coordenadas (x,y) del impacto de la piedra son dos números al azar.
Repito el experimento muchas veces, con la idea de que cuando más veces mejor (¿Esto será bueno?)
Calculo la frecuencia de que la piedra caiga dentro del círculo.
Es decir:
\(frec= \frac{piedras\ en\ el\
c\acute{i}rculo}{total\ de\ piedras}\)
Viendo este experimento ¿Cuál es la probabilidad de que una piedra
quede dentro del círculo?
\[Prob = \frac{Casos\ favorables}{Total\ de\
casos} = \frac{\acute{A}rea\ del\ c\acute{i}rculo}{\acute{A}rea\ del\
cuadrado}\]
Reemplazando áreas por su expresiones y haciendo las cuentas
\[Prob = \frac{\pi R^2}{(2R)^2} = \frac{\pi}{4}\]
Si suponemos (aunque sabemos que se le parecen pero no son lo mismo) que la frecuencia medida es la probabilidad de que la piedra caiga en el círculo, obtenemos que:
\(frec \sim \frac{\pi}{4}\) y si despejo \(\pi\) obtengo \(\pi \sim 4 frec\) donde la frecuencia la obtengo a partir de la simulación. Pero para que esto funcione tenemos que hacer que la frecuencia realmente se parezca a la probabilidad y para que esto suceda tenemos que repetir el experimento muchas veces (¡quizás varios millones de veces!).
Veamos cómo sería un programa que realice toda esta tarea. Genere los dos números al azar, vea si estás coordenadas están dentro del círculo, actualice los contadores (piedras en el círculo y cantidad total de piedras), nos de un estimado del valor de \(\pi\) que obtuvimos hasta el momento y vuelva a repetir la operación una y otra vez.
\(\ \ \ \ \ \ \ \)program pi_con_azar
c Inicializo
\(\ \ \ \ \ \ \ \)real*8 x,y,xf,pi,puntos,puntosc
c xf es la semilla recomendada para una serie muy larga de números al azar en
c este generador
\(\ \ \ \ \ \ \ \)xf=0.3846293861039840D15
\(\ \ \ \ \ \ \ \)n1=0
\(\ \ \ \ \ \ \ \)puntos=0.
\(\ \ \ \ \ \ \ \)puntosc=0.
\(\ \ \ \ \ \ \ \)
c Calculo la simulación de arrojar una piedra y la cuento en “puntos”
c Si cae dentro del círculo, además la cuento en “puntosc”
10 \(\ \ \ \)continue
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)call azar(xf,x)
\(\ \ \ \ \ \ \ \)call azar(xf,y)
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)puntos=puntos+1
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)if (x**2+y**2.le.1) then
\(\ \ \ \ \ \ \ \ \ \)puntosc=puntosc+1
\(\ \ \ \ \ \ \ \)endif
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)pi=puntosc/puntos*4
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)n2=puntos/1000000
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)if(n2.gt.n1) then
\(\ \ \ \ \ \ \ \ \ \ \)call escribir(n2,pi,puntos)
\(\ \ \ \ \ \ \ \ \ \ \)n1=n2
\(\ \ \ \ \ \ \ \)endif
\(\ \ \ \ \ \ \ \)goto 10
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)end
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)subroutine escribir(n2,pi,puntos)
\(\ \ \ \ \ \ \ \)real*8 puntos,pi
\(\ \ \ \ \ \ \ \)error=1./sqrt(puntos)
\(\ \ \ \ \ \ \ \)write(*,*) ’pi=’,pi,’ con ’,n1,’millones de puntos con un error
\(\ \ \ \ \ \)#de’,error
\(\ \ \ \ \ \ \ \)return
\(\ \ \ \ \ \ \ \)end
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)SUBROUTINE AZAR(Y,X)
\(\ \ \ \ \ \ \ \)REAL*8 X,Y
\(\ \ \ \ \ \ \ \)Y=65539D0*Y
\(\ \ \ \ \ \ \ \)Y=DMOD(Y,2147483647D0)
\(\ \ \ \ \ \ \ \)X=Y*4.65661287524D-10
\(\ \ \ \ \ \ \ \)RETURN
\(\ \ \ \ \ \ \
\)END
La subrutina escribir() se encarga de justamente
imprimir en pantalla el valor parcial de \(\pi\) conseguido hasta el momento. Es
llamada cuando el valor del número de simulaciones cambia el dígito del
millón. De esa manera se consigue que el programa funcione más rápido.
Escribir en pantalla consume muchos recursos de la computadora y en este
caso no es necesario que se haga todo el tiempo. Y esos recursos van
ahora a ser usados en que la simulación corra más rápido.
El error en la simulación se lo considera como Poissoniano (cumple con
la distribución de Poisson) y por lo tanto para N eventos el error
relativo es \(error=1/\sqrt{n}\).
La tabla 12.1 son los resultados para distintas cantidades de simulaciones de piedras arrojadas.
| # de piedras | Valor de \(\pi\) obtenido | Error estadístico |
|---|---|---|
| \(10^6\) | 3.1424319999999999 | \(1.00000005\ 10^{-3}\) |
| \(10^7\) | 3.1407848888888887 | \(3.33333330\ 10^{-4}\) |
| \(10^8\) | 3.1416244799999999 | \(9.99999975\ 10^{-5}\) |
| \(10^9\) | 3.1415663320000000 | \(3.16227779\ 10^{-5}\) |
| \(10^{10}\) | 3.1416044472000002 | \(9.99999975\ 10^{-6}\) |
| \(10^{11}\) | 3.1415875904799999 | \(3.16227761\ 10^{-6}\) |
| \(10^{12}\) | 3.1415921563320000 | \(9.99999997\ 10^{-7}\) |
| \(10^{13}\) | 3.1415922104799999 | \(3.16227761\ 10^{-7}\) |
Uno de los problemas que provocó una de las mas ricas discusiones en
la creación de algoritmos fue la búsqueda de métodos que sirvan para
realizar programas que ordenen la información. Es decir, por ejemplo
ordenar de mayor a menor (o al revés), una tabla a partir de una de sus
columnas. Para simplificar el problema sólo trataremos el caso de
ordenar las componentes de un vector. Los métodos más simples que
permiten entender la complejidad del problema son el método de la
Burbuja y el de Selección. Pero a la hora hora de ordenar grandes
cantidades de información son desaconsejados por su lentitud e
ineficiencia.
Si la información se encuentra en un vector, el método de selección
se basa en la idea de tomar el primer elemento del vector y compararlo
contra todos los otros elementos. Si ordenamos de mayor a menor y este
primer elemento es menor que el elemento contra el cual estoy comparando
lo cambio por este. Una vez hecho este cambio sigo ahora comparando mi
nuevo primer elemento contra los otros elementos restantes, continuando
con la idea de que cada vez se cumpla con encontrar otro menor se vuelve
a realizar el cambio. Para realizar el cambio del elemento se debe usar
una variable temporaria ( temp en el programa). Una vez
terminada la comparación del primer elemento tomo el segundo y así
continuo el proceso de comparación contra los elementos restantes. Este
ciclo termina cuando comparo el anteúltimo elemento contra el último.
Con este algoritmo se va coleccionando los elementos más grandes en los
primeros elementos del vector.
El tiempo que tarda este procedimiento es proporcional a \(t \sim N^2\) (donde N es la cantidad de
elementos a ordenar). Por lo tanto, el tiempo crece muy rápido si se
aumenta la cantidad de elementos a ordenar. Por ejemplo, si duplico la
cantidad de elementos a ordenar tardaré 4 veces más, pero en el caso de
tener 10 veces mas elementos tardaré 100 veces más en obtener un
resultado útil. No es un método aconsejable para usar en una situación
real, pero tiene utilidad académica, ya que sirve para entender los
procesos y problemas involucrados en los algoritmos usados para
ordenar.
El programa que realiza esta tarea sería el siguiente:
\(\ \ \ \ \ \ \ \)subroutine
selec(n,a)
\(\ \ \ \ \ \ \ \)real*4 a(10000000)
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)do i=1,n-1
\(\ \ \ \ \ \ \ \ \ \)do j=i+1,n
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \ \ \ \ \)if(a(i).lt.a(j)) then
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \)temp=a(i)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \)a(i)=a(j)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \)a(j)=temp
\(\ \ \ \ \ \ \ \ \ \ \ \)endif
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \ \ \)enddo
\(\ \ \ \ \ \ \ \)enddo
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)return
\(\ \ \ \ \ \ \ \)end
El método de la burbuja se basa en la idea de comparar sólo entre
pares cercanos e intercambiar los valores cuando cumplen con la
condición deseada (mayor o menor valor según el orden que esté
buscando). Este ciclo se tiene que repetir al menos n-1 veces si n es el
número de elementos a ordenar. Pero se puede programar que si no se
produce ningún cambio en uno de los ciclos (esto sucede cuando el vector
ya quedó ordenado) que no se continue el proceso, ahorrando tiempo de la
computadora. Para testar si dejó de haber cambios, uso la variable
lógica bandera en el programa. Esta variable toma el
valor .true. mientras se siguen haciendo cambios y .false cuando ya el
vector está ordenado. En este último caso el programa termina.
El programa que realiza esta tarea sería el siguiente y es relativamente
sencillo:
\(\ \ \ \ \ \ \ \)subroutine
bubble(n,a)
\(\ \ \ \ \ \ \ \)real*4 a(10000000)
\(\ \ \ \ \ \ \ \)logical bandera
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)bandera=.true.
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)do while(bandera)
\(\ \ \ \ \ \ \ \ \ \)bandera=.false.
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \ \ \)do i=1,n-1
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \ \ \ \ \)if(a(i).gt.a(i+1)) then
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \)temp=a(i)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \)a(i)=a(i+1)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \)a(i+1)=temp
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \)bandera=.true.
\(\ \ \ \ \ \ \ \ \ \ \ \)endif
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \ \ \)enddo
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)enddo
\(\ \ \ \ \ \ \ \)return
\(\ \ \ \ \ \ \
\)end
Este método va con \(t \sim N^2\) y al
igual que el método de selección no es para nada bueno, por no decir que
es bastante malo, en lo que hace a su eficiencia. Se tiene como única
ventaja que el algoritmo termina abruptamente si encuentra el vector
ordenado y por lo tanto es mejor que el método de selección. Este último
no sería capaz de descubrir que el vector ya está ordenado y repetiría
todos los pasos hasta el final aún con un vector ordenado.
Hay otros métodos que son mejores. Veremos algunos de ellos, pero no con profundidad. Para el lector con mayor interés en el tema se puede consultar el libro Numerical Recipes (ya nombrado anteriormente). Este libro se puede consultar aquí. El texto consta de explicaciones de los algoritmos primero en forma teórica y luego práctica, en la cual se incluye la subrutina del método escrita en Fortran. En este libro hay mucha información detallada con explicaciones y evaluaciones de la eficiencia de los métodos que nombraremos y otros mas.
Este método viene del modo más simple de ordenar un mazo de cartas. Se toma la segunda baraja y se la compara con la primera, si hay que cambiarla, se la cambia. Se toma la tercera y se compara con la segunda y luego con la primera. Se sigue así hasta la última carta. Hay que notar que no es necesario comparar contra todas las cartas, solo hasta que se encuentre el lugar que le corresponde, lo que ahorra tiempo de computación. Este método va con \(N^2\) (en el caso extremo) y se aconseja su uso para muestras pequeñas (\(\sim N < 20\)). Se lo utiliza como apoyo de otros algoritmos para ordenar subgrupos parciales de un grupo mayor, porque para pocos elementos es eficiente y rápido.
Esta es en si una variante del método anterior. La idea es dividir la muestra en grupos de a dos, ordenar estos elementos en el grupo de a dos usando inserción directa. Y luego juntar en ahora grupos de 4 elementos ordenar y juntar en grupos del doble de elementos y repetir el proceso. Se puede mostrar que en promedio que en este método el tiempo va como \(t \sim N^{1.25}\) al menos para \(N<60000\). El truco de este algoritmo es que se puede ordenar muy rápido grupos de pocos elementos y si junto grupos que ya están algo ordenados el algoritmo tiene pocas veces que cambiar elementos de lugar, es decir aumento la probabilidad de que un elemento ya esté en su lugar. Y por ello en promedios el método es más rápido que \(N^2\).
Este método es el más rápido conocido para muestras muy grandes que se necesita ordenar, la idea es que la muestra se parte en dos pedazos y un elemento en particular (el \(a\)) es el seleccionado para separar estas dos particiones. Los elementos son chequeados en pares dejando en una muestra los elementos \(\leq\) a la izquierda y en la otra los \(\geq\) a la derecha, por lo tanto \(a\) queda en su lugar. El proceso se vuelve a repetir con la partición de la izquierda y luego con la de la derecha. Para realizar toda esta tarea el algoritmo requiere algo más de memoria, pero es extremadamente eficiente. Este método es algo mejor que otro método conocido como Heapsort que también muestra un excelente desempeño para grandes valores de \(N\).
r0.30 
Para probar los distintos métodos haremos un programa que ordene un
vector de elementos al azar y mediremos los tiempo de cada algoritmo y
su implementación. Pero hay que señalar un punto importante, los
distintos métodos, tienen distintos resultado según las características
de los datos de entrada. Puede haber datos desordenados al azar (como lo
que vamos a usar en el ejemplo), datos con cierto grado de ordenamiento
y datos que estén completamente invertidos en su distribución, es decir,
quiero ordenar de menor a mayor pero los datos originales están ya
ordenados de mayor a menor (o parcialmente ordenados). La eficiencia de
los algoritmos puede en si cambiar bastante según esta distribución de
datos de entrada.
Para esto utilizaremos las rutinas del método de selección y el de la
burbuja que hemos visto, y las demás implementaciones serán del
Numerical Recipes. La tabla 12.2 muestra
los tiempos que tarda en hacer los cálculos cada uno de los algoritmos
descriptos sobre la misma muestra. En la figura [fig:qr_sort]
pueden verse una comparación de distintos métodos como animación en
tiempo real de ellos.
| Algoritmo | \(10^5\) números | \(10^6\) números |
| segundos | segundos | |
| Burbuja | 36.07 | 3678.71 |
| Selección | 25.95 | 2547.27 |
| Inserción Directa | 6.56 | 646.6 |
| Cáscaras | 0.02 | 0.3 |
| Heapsort | 0.02 | 0.19 |
| Quicksort | 0.01 | 0.12 |
Si tengo pares ordenados (\(X_i\),\(Y_i\)) y por ejemplo los ordeno por los
valores \(X_i\). Es necesario que los
pares ordenados no se destruyan o sea que cada \(X_i\) sigan asociados a su \(Y_i\). Para resolver este problema deberé
agregar a la subrutina no importa cual sea el método que cuando cambio
el elemento \(X_i\) cambie también el
\(Y_i\), de esta manera:
\(\ \ \ \ \ \ \ \)\(\vdots\)
\(\ \ \ \ \ \ \ \)IF(algo) then
\(\ \ \ \ \ \ \ \)temp=X(i)
\(\ \ \ \ \ \ \ \)X(i)=X(i+1)
\(\ \ \ \ \ \ \ \)X(i+1)=temp
\(\ \ \ \ \ \ \ \)temp=Y(i)
\(\ \ \ \ \ \ \ \)Y(i)=Y(i+1)
\(\ \ \ \ \ \ \ \)Y(i+1)=temp
\(\ \ \ \ \ \ \ \)\(\vdots\)
El “algo” que aparece en el IF dependerá del algoritmo a utilizar.
Una posibilidad es ordenar pero sin modificar el vector inicial y sin
copiarlo a otro vector. Para hacer esta tarea creamos un vector de
índices, donde el primer elemento tiene un 1, el segundo un 2 y así
hasta los N valores que sean necesarios.
Si A es el vector a ordenar e I es vector de índices, puede referirse a
los elementos de A como A(I(j)), es decir cada elemento de A, será el
elemento i(j). Entonces en vez de ordenar el vector A, modifico los
índices del vector I y de esta manera puedo mantener la configuración
inicial de A y también la forma ordenada como A(i(j)).
Es decir haríamos:
\(\ \ \ \ \ \ \ \)\(\vdots\)
\(\ \ \ \ \ \ \ \)IF(algo) then
\(\ \ \ \ \ \ \ \)temp=I(j)
\(\ \ \ \ \ \ \ \)I(j)=I(j+1)
\(\ \ \ \ \ \ \ \)I(j+1)=temp
\(\ \ \ \ \ \ \ \)\(\vdots\)
Y el vector A no lo tocamos, sólo modificamos el vector de índices.
Estas son llamadas a subrutinas del propio sistema operativo y son
muy útiles.
GETARG() permite ingresar datos para las variables en el mismo renglón
que se llama al programa, mientras que GETENV() permite obtener
parámetros del ambiente del usuario (ejemplo, su nombre, directorio en
el que está, etc).
Para GETARG() tenemos que dar como argumentos el número de la variable
que voy a leer en la línea de programa y una variable de caracter donde
quedará escrita esa variable.
En cambio para para GETENV() deberé indicar el nombre de la variable de
ambiente que leo y una variable de caracter donde quedarán escritos esos
datos.
Ejemplo:
\(\ \ \ \ \ \ \ \)program
prueba
\(\ \ \ \ \ \ \ \)character name*32, argument*32
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)call getenv(’USER’,name)
\(\ \ \ \ \ \ \ \)call getarg(1,argument)
\(\ \ \ \ \ \ \ \)
\(\ \ \ \ \ \ \ \)write(6,*) ’Username=’,name
\(\ \ \ \ \ \ \ \)write(6,*) ’Argument=’,argument
\(\ \ \ \ \ \ \
\)end
Y si compilo y luego corro el programa así:
./prueba 22
obtengo como resultado:
Username=carlos
Argument=22
Esta llamada permite dar órdenes al sistema operativo con los
comandos de texto como si fuesen escritos en una terminal. Saber usar
esta llamada tiene muchas ventajas. Normalmente existen más de 3000
comandos en una instalación simple de LINUX. y muchos cubren la mayoría
de los necesidades domésticas, como transformar archivos de formatos,
etc. En resumen, un programa Fortran puede darle órdenes al sistema
operativo.
Por ejemplo, si quiero que mi programa lea del directorio los archivos
que terminen en “.dat” para después procesarlos haría:
\(\ \ \ \ \ \ \ \) \(\vdots\)
\(\ \ \ \ \ \ \ \)CALL SYSTEM(’ls *.dat > mis_archivos.txt’)
\(\ \ \ \ \ \ \ \)OPEN(45, file=’mis_archivos.txt’)
\(\ \ \ \ \ \ \ \) \(\vdots\)
Entonces en mis_archivos.dat tendría la información requerida.
Los lenguajes de computación modernos están en una evolución permanente y se realizan cambios importantes todo el tiempo. La idea de este capítulo (y de la clase correspondiente) es sobre como encarar el hecho de enfrentarnos en un nuevo trabajo o proyecto a un lenguaje de programación que no conocemos. Lo que hay que entender es que si bien los lenguajes pueden ser distintos hay estructuras y formas de construir las órdenes que se repiten entre las diferentes maneras de programar. Por lo tanto con identificar estas estructuras ya está hecho mucho del trabajo de aprender un nuevo lenguaje. Por otro lado, conocer y entender las formas abstractas que tienen en común todos los lenguajes habla de la versatilidad que uno tiene a adaptarse a nuevos desafíos.
r0.30 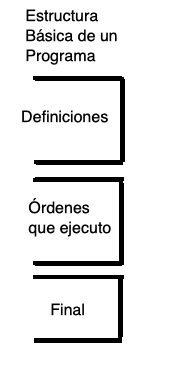
Hay tres estructuras básicas en todo lenguaje, las dos primeras las
hemos visto en Fortran. La primera son las definiciones: que variable es
de cada clase, si las variables son enteras, reales, son arreglos (así
se suele llamar a la matrices y vectores), variables lógicos. En algunos
lenguajes es obligatorio definir todas las variables, en otros no y son
por ejemplo todas las variables son real*8 a menos que se especifique lo
contrario. Algunos como el Python reconocen el tipo de variable según el
valor o texto que uno le asigna por primera vez.
La segunda estructura es el programa en si, son la colección de órdenes
que quiero que el programa ejecute. En este lugar hay que entender como
se escriben las sentencias en el lenguaje, como se hacen las
asignaciones y los nombres de funciones intrínsecas (o procedimientos o
como se llamen este lenguaje) y la manera de crear y definir mis propias
funciones. Sobre estos puntos hablaremos en la sección que sigue.
La tercera parte de la estructura es lo que se debe hacer cuando el
programa termina, y en Fortran no tenemos órdenes en este espacio, salvo
uno podría pensar que la orden CLOSE() que cierra
archivos, pero no necesariamente va la final del programa en Fortran.
Hay lenguajes donde se especifica trabajo a realizar cuando el programa
ya ejecutó las órdenes de la segunda etapa
Como vimos el Fortran es un lenguaje compilado a diferencia de otros
lenguajes que son interpretados. Existen lenguajes híbridos en el
sentido de que pueden interpretarse, compilarse o bien correr una parte
del programa y no su totalidad. En algunas ocasiones en los programas
interpretados hay que correr el interprete primero: “Intérprete
programa”, es decir el intérprete es el programa que se corre y lee las
órdenes del archivo “programa”. Ejemplo: escribo “python
mi_programa.py”, donde “python” es el intérprete y “mi_programa.py” es
el código a correr. Hay lenguajes interpretados que van guardando las
órdenes ya compiladas entonces se vuelven rápidos en algunas situaciones
particulares, por ejemplo, de bucles o lazos.
Muchas veces los programas tienen sistemas o ambientes donde se los
edita, compila o interpreta, a esos sistemas se los denomina SDK
(Software Development Kit). Existen lenguajes que pueden correrse
entornos que son páginas web, la cursada no presencial hemos indicado
una de estas páginas web que pueden correr Fortran. Pero existen
estructuras más sofisticas que permiten ejecutar programas no en forma
completa sino en segmentos llamados celdas. Es decir divido mi programa
en celdas y las voy corriendo de a una. Estos sistemas incluso son
capaces de devolver como resultado figuras y videos. Ejemplo: Python
siendo corrido en un notebook.
También los lenguajes suelen tener programas auxiliares al compilador
para encontrar errores. Este trabajo se suele llamar debugging o sea
encontrar bugs (errores en el código). En el Linux está el programa
ftnchek para encontrar problemas en el Fortran.
Vimos que en Fortran se usa el “=” para asignar un resultados a una
variable, la mayoría de los lenguajes con base en cálculo lo usa, pero
lenguajes más relacionados con las matemáticas formales lo evitan, a
veces usan “:=” , “<-” o símbolos parecidos. En algún caso hay
órdenes especificas como “Set a b+2”, entonces b+2 se asigna a la
variable a. En lenguajes como Perl las variables para diferenciarlas de
las funciones, órdenes y texto en general llevan el signo “$” adelante
del nombre ($i = $b +1).
La variables en mayúsculas o minúsculas pueden ser consideradas como
diferentes en algunos lenguajes, es decir “MAG” ,“Mag” y “mag” son tres
variables distintas en un mismo programa (en Fortran son la misma
variable).
En algunos lenguajes existen versiones resumidas para órdenes muy
usadas. Por ejemplo, i = i+1, se puede escribir como
i++. Esta forma de escritura se realiza con el fin
realizar menos operaciones a nivel de la cpu y por lo tanto consumir
menos recursos de la computadora.
Por lo cual, podría poner C = B*(i++), esta
sentencia ordena multiplicar B*i y luego asignarlo a C. Pero después de
esa acción se realiza una segunda operación la cual es sumar 1 al valor
de i. Es decir en un sólo renglón tengo dos operaciones diferentes y un
orden en cual realizarlas. Si quisiera hacerlas en el orden inverso
tendría que poner C = B*(++i). Entonces ahora se suma 1 a i y luego se
lo multiplica por B y se lo asigna en C. También se pueden hacer otras
operaciones resumidas, estás son:
i\(--\) resto un 1 en vez de
sumar
A+= 3 que es equivalente a A = A+3
B*= 5.4 que es equivalente a B=B*5.4
D/= 3.1415 que es equivalente a D = D/3.1415
La mayoría de los lenguajes modernos permiten escribir sentencias empezando desde la columna 1 y no tienen límite de cantidad de caracteres. Obviamente no es muy conveniente tener sentencias muy largas. En algunos lenguajes hay que indicar el final de la sentencia con por ejemplo un“;”. También las sentencias puede ser agrupadas utilizando llaves en grupos “{}” cuando es necesario por alguna razón como por ejemplo ser parte de IF(). En Python por toda sentencia con algún tipo de sangría (no comienza en la primer columna) indica que es parte de una estructura. Una segunda estructura (por ejemplo, otro IF/() dentro de este tendría una sangría más larga. Es decir igual sangría indica la pertenencia a la misma estructura.
Como hemos visto en el Fortran la letra C al comienzo de una línea
indicaba que dicha sentencia era un comentario y por lo tanto
información no ejecutable como orden. En todos los lenguajes existen
órdenes para indicar comentarios. La más popular en casi todos los
lenguajes es el símbolo “#”, por ejemplo en Python, Perl y muchos
lenguajes asociados al sistema operativo UNIX. En Fortran 90/95 se
prefiere que el comentario se indique como “!”, aunque esto no se ha
visto como buena idea, ya que el símbolo de admiración es considerado
como la orden de negación lógica (NOT) en una vasta variedad de
lenguajes. El lenguaje Basic y variantes de este utilizan la orden REM
para los comentarios. El lenguaje de procesamiento de textos TeX y su
variante LaTeX usan el signo “%” que se puede poner en el comienzo o en
cualquier parte de la línea y de ahí en adelante todo lo que sigue en
ese renglón es un comentario.
Hay lenguajes que tienen una orden específica para el comienzo del
comentario y de ahí en adelante todos los renglones hasta otra orden que
cierra el comentario no son ejecutables. Como por ejemplo, el “\”
comienza el comentario y el bloque se cierra con un “*/” en lenguajes C
y relacionados. En HTML (lenguaje de las páginas web), el comentario
comienza con “<!–” y se cierra con “–>”. Python incluso tiene un
lenguaje asociado llamado markdown que es una versión muy simplificada
de LaTeX para realizar comentarios. En resumen, todos los lenguajes
tienen la manera de indicar líneas de información que no son parte
ejecutable del programa.
Además, de los arreglos en muchos lenguajes modernos existen otros
tipos de variables con estructuras. Por ejemplo:
listas, estas son exactamente eso listas de elementos,
sin necesidad de entenderlos como un vector. Existen lo que se llama
diccionarios, donde una variable está asociada según la
información que se pide, a otra que tiene asignada. Veremos algunos de
estos tipos de variables en la parte del curso que tratemos
Python.
En la mayoría de los lenguajes para los arreglos no se usan los “()”, ya
que se los dejan para los argumentos de las funciones, entonces para
indicar los elementos de un arreglos se usan los “[]”. Por ejemplo A[I],
o B[i,j]. En si hay dos formas de indicar las filas y columnas en los
arreglos, la forma que hemos usada en esta cursada que es la manera que
se usa en álgebra y conocida en informática como el estilo “Fortran",
donde número filas y columnas, o el estilo “C" donde un arreglo
bidimensional es un arreglo unidimensional cuyos elementos son otros
arreglos unidimensionales. En python algunos comandos dan la opción de
elegir entre estos dos estilos.
La sentencia IF es clásico en cualquier lenguaje y además se la usa
de la misma forma en todos los lenguajes. La única diferencia es que
normalmente el que no existe es el ENDIF. Pero si existen el ELSE,
ElIF() (o ELSEIF() según la gramática del lenguaje) para hacer preguntas
secundarias. En lenguajes mas modernos suele utilizar los símbolos
<,>,>=,<=,== (igual), != (no es igual), este último en
Fortran 90/95 suele escribirse como /=. Las órdenes internas dentro de
un IF se agrupar con “{}”, o son las órdenes que comparten la misma
sangría (veremos esto más adelante al estudiar Python). En este último
caso un cambio de sangría indica que el IF() terminó. Ejemplo:
IF(a<b) {
\(\ \ \ \) algo}
else {
\(\ \ \ \) algo2 }
Con respecto a los operadores lógicos, existen muchos lenguajes donde
&& (o un sólo &) es el .AND. de Fortran, || (o uno sólo |)
es el .OR. y ! es el .NOT.
En algunos lenguajes se usa el DO con una orden muy parecida al
Fortran, pero en vez de DO es la orden FOR. En lenguajes como BASIC y
variantes es igual al DO de Fortran. Pero en lenguajes más modernos el
FOR se usa en una forma parecida conceptualmente pero con una gramática
muy diferente.
Por ejemplo: FOR(i=0; i<10; i++){ acá van todos las sentencias que se
repiten }
En este ejemplo, i se inicia en 0, el último valor que tomará será 9,
por eso se pregunta i<10 y el i++ es que el paso es 1, es decir se
suma 1 a i en cada loop. Una ventaja apreciable en esta forma de
escribir es que el paso puede ser modificado con una formula matemática
pudiéndose avanzar con pasos logarítmicos o exponenciales. En los
lenguajes donde existen listas se puede realizar una sentencia FOR que
se aplica a todos los elementos de una lista.
Algunos lenguajes recomiendan utilizar vectores y operaciones
vectoriales con el fin de evitar los loops, esto se debe a que esas
operaciones se hacen mucho más rápido de esta manera que tener que
repetir la interpretación de los comandos una y otra vez durante todo el
bucle. Esto es especialmente ciertos lenguajes como Matlab/Octave,
Python (utilizando Numpy) y R. Esto no sucede en lenguajes compilados o
en aquellos que sólo interpretan la primera vez que corre el lazo, por
ejemplo, el lenguaje Julia.
El Do While es similar en su utilización al que vimos en Fortran. Pudiéndose en poner incluso la pregunta al final, de esta manera Do {algo} while (a>10.5) con un funcionamiento similar al que conocemos.
Repeat, repite un lazo a ciegas, no hay comienzo ni final, salvo
porque en algún momento (seguramente usando la sentencia if()) se activa
un break que termina el bucle.
repeat {
\(\ \ \ \) IF(a<b) { break }
}
}
El programa queda atrapado en el lazo hasta que el break lo
libera.
El comando next es para que la variable de un loop siga con el próximo
valor, es decir, el actual por alguna razón se descarta.
Try se usa para ver si una actividad sucedió sin errores, esta
actividad es la está dentro del “Try”. Pero si sucedieron errores se
puede en la orden “Except” indicar que hacer en el caso particular de un
error determinado. La estructura sería de la siguiente manera:
Try {
}
Except algún tipo de error {
}
Las formas posibles del “tipo de error” para la orden “Except” están
previamente determinado en el lenguaje y sus nombres están listados en
los manuales del lenguaje en particular.
En todos los lenguajes encontraremos algo parecido a Funciones o Subrutinas que a veces son una mezcla de ambas y cumplen con las mismas reglas de memoria que hemos visto y por lo tanto se las puede usar en forma recursiva. Si el lenguaje es interpretado es necesario que la definición de estas esté al comienzo del programa para que el sistema “aprenda” y por lo tanto conozca nuestra función antes de que se la intente utilizar.
La mayoría de los lenguajes no tienen funciones intrínsecas integradas, hay que cargar una bbilioteca de matemática (a veces al comienzo del programa) si uno quiere utilizarlas. Es decir no existen funciones como la raíz cuadrada, o la trigonometría a menos que uno la indique específicamente.
Algunos lenguajes no traen todas las funciones trigonométricas
definidas. Es decir sólo tienen el \(sen()\), \(cos()\) y \(arctan()\). Es decir el usuario se debe
arreglar con estas 3 para todas las demás. Para calcular la tangente
debo hacer \(\tan(x)=\cos(x)/\sin(x)\).
y para el arcseno() debo calcularlo como: \(x
= arcsen(y)=arctan(y/\sqrt{1-y^2})\), mientras que el arccos()
como \(arccos(y)=arctan(\sqrt{1-y^2}/y)\). ¿Cómo
se llega estas expresiones? De esta manera:
Esto sale de que \(y=cos(x)\) y \(\tan(x)=cos(x)/sen(x)\)
\(\tan(x)=cos(x)/\sqrt{1-cos^2(x)}\)
reemplazando y tomando el arctan() queda:
\(x = arctan(y/\sqrt{1-y^2})\)
y de manera similar se consigue la expresión para el arcsen(x).
En el caso de los logaritmos puedo que sólo esté definido el logaritmo
natural. Entonces para utilizarlo en otra base (b) deberé hacer \(log_b(x) =\ln(x)/ln(b)\). Si quiero el
logaritmo decimal lo puedo entonces calcularlo a partir de los
naturales: \(log_{10}(x)=ln(x)/ln(10)\)
En física, con un vector con 3 componentes podemos describir la
posición de una partícula en el espacio y con otro vector de 3
componentes podemos describir su velocidad. En programación orientada a
objetos, un objeto es algo parecido, pero su estructura de componentes
es más compleja. Imaginémonos ahora los datos que tiene la Facultad de
cada alumno del Observatorio. Esos datos dan una descripción como si
fuese un vector que apunta a cada alumno. Es decir, figura el DNI, la
dirección de su casa, una serie de datos personales, etc. Algunos de
esos datos, a su vez tiene subestructura, por ejemplo la fecha de
nacimiento que se divide en tres: día, mes y año, o datos no numéricos
como el nombre y el apellido.
Es decir un objeto es un vector, bastante más complejo de los que
estamos acostumbrados del álgebra y de la física. La idea principal es
que la programación orientada a objetos conecta los datos, sus
propiedades y distintas acciones que puedo hacer con ellos. Veamos la
nomenclatura y conceptos:
Clase: Se llama clase a la definición con la cual se crea el
objeto. En nuestro ejemplo, la Universidad decidió qué datos son los que
debería saber de sus alumnos, con esos datos creó la clase. Esta es una
definición abstracta. Ya que la clase no es el objeto, sino la forma y
la definición.
Objeto: Es cuando yo aplico la clase para crear algo real, por
ejemplo creo un objeto con la definición de la clase que lo puedo llenar
con los datos de un alumno en particular. Crear el objeto se denomina
como “la instancia".
Atributos: Son datos que están en el objeto que nos describen características del objeto. Por ejemplo, si el objeto es un vector, un atributo normalmente, sería su tamaño. Es decir el objeto, es este caso el vector sabe cuántos elementos tiene. Estos atributos existen, porque fueron definidos con la clase.
Métodos o Funciones: Los objetos tienen funciones predefinidas que se construyen con la clase. Por ejemplo, podría tener asociado a un vector una función que sume todos sus elementos y otra función que me calcule el módulo del vector. La funciones están definidas en la clase pero sólo se ejecutan con un orden del código del programa, en el momento en que se pide su activación, si no se la requiere no se ejecuta.
Nomenclatura: Si tengo un vector A que es un objeto en mi programa, podría llamar a los elementos individuales como A[n], donde n sería el número de este elemento. Si el atributo de su tamaño está definido en la clase con el nombre size, A.size me daría el tamaño. Si tuviese la función de la suma de componentes del vector definido en la clase con nombre sum, A.sum() calcularía la suma porque estoy llamando a esa función. El atributo siempre tiene un valor ya determinado, la función en un objeto se calcula en el momento que la pido. En Python, por ejemplo, además su nombre tiene los paréntesis indicando que es función (hay excepciones, pero en general es la manera de distinguir entre atributos y funciones). Dentro de los paréntesis se pueden entregar parámetros para la ejecución de la función.
Nomenclatura 2. Si tengo el objeto alumno, y dentro de este objeto esta el “número de alumno” y se llama numero, alumno.numero será esa variable. Es decir que el objeto.algo me permite acceder a ese variable en particular. Siendo incluso tan complejo como lo necesite la estructura. Pudiendo tener por ejemplo, alumno.fecha.día, alumno.fecha.mes y alumno.fecha.año
Los caracteres se pegan con una operación cuyo orden en Fortran es
“//”.
Ejemplo:
\(\ \ \ \ \ \ \ \) character*5
parcial,A,B
\(\ \ \ \ \ \ \ \) character*15 C
\(\ \ \ \ \ \ \ \) A = ’El no’
\(\ \ \ \ \ \ \ \) B = ’ esta’
\(\ \ \ \ \ \ \ \) C = A//B//’ aqui’
\(\ \ \ \ \ \ \ \)
write(*,*) C
Si corremos este código, obtendríamos el siguiente texto:
El no esta aqui
Como vemos puedo pegar variables de caracter e incluso textos
delimitados por el símbolo ’.
En cambio para cortar solo se debe indicar la parte del texto que
quiero, indicando el número del primer caracter y el último separados
por el símbolo“:”. Si en el primer número no pongo nada se sobreentiendo
que es el primer caracter. Si en el segundo número tampoco pongo nada se
entiende que es hasta el último caracter.
\(\ \ \ \ \ \ \ \) character*32
cartel
\(\ \ \ \ \ \ \ \)
character*5 parcial
\(\ \ \ \ \ \ \ \) cartel=’La
serie empieza en el número 82’
\(\ \ \ \ \ \ \ \) parcial=cartel(:5)
\(\ \ \ \ \ \ \ \)
write(*,*) parcial
\(\ \ \ \ \ \ \ \)
parcial=cartel(5:10)
\(\ \ \ \ \ \ \ \)
write(*,*) parcial
\(\ \ \ \ \ \ \ \)
parcial=cartel(28:)
\(\ \ \ \ \ \ \ \)
write(*,*) parcial
Y se corro este código obtengo:
La se
erie
ro 82
Los números pueden ser escritos como números en la computadora (transformado en binario) y con ellos realizar todas las operaciones matemáticas o pueden estar escritos como texto y son letras sin posibilidad alguna de realizar ningún cálculo sobre ellos. Muchos formatos utilizados para el transporte y posterior archivado de datos suelen llevar encabezamientos con información sobre estos escritos en texto con indicaciones numéricas de por ejemplo, como se tomaron esos datos y en que condiciones. Puede ser entonces que se los requiera convertir en números o bien a la inversa que se quiera guardar datos en uno de esos formatos y realizar la operación inversa, convertir los números a texto.
Si tengo un número escrito como un texto y lo quiero convertir a
número binario puedo hacer lo siguiente:
\(\ \ \ \ \ \ \ \)Character*20
naxis
\(\ \ \ \ \ \ \ \) \(\vdots\)
\(\ \ \ \ \ \ \ \)READ(naxis,100) NX
100 \(\ \
\)Format(A20)
En este caso, estaríamos reemplazando la UNIDAD LOGICA que es un número
que indica el lugar donde leo por la variable naxis, es decir se indica
que leo de esa variable y escribo sobre NX que es una variable
entera.
Para ello realizo la operación inversa la ejemplo anterior, en vez de
leer (READ) escribo (WRITE) y entonces sería así el comando:
\(\ \ \ \ \ \ \ \)Character*20
char
\(\ \ \ \ \ \ \ \) \(\vdots\)
\(\ \ \ \ \ \ \ \) WRITE(char,101) NY
101 \(\ \ \)
Format(I4)
La sentencia EQUIVALENCE proviene de las épocas cuando las
computadoras tenían poca memoria y permite que dos variables con nombres
diferentes apunten a la misma memoria. Si escribo:
\(\ \ \ \ \ \ \ \)REAL*4
A(5),C(3)
\(\ \ \ \ \ \ \
\)EQUIVALENCE(A(3),C(1))
Estas son órdenes hacen que A(3) y C(1) apunten a la misma memoria ram.
Pero la orden se propaga por ls vectores así que A(4) y C(2) son lo
mismo y A(5) y C(3).
Haciendo un esquema:
\(\ \ \ \ \ \ \ \) A(1) \(\leftarrow \rightarrow\) Sólo se usa con
ese nombre
\(\ \ \ \ \ \ \ \) A(2) \(\leftarrow \rightarrow\) Sólo se usa con ese nombre
\(\ \ \ \ \ \ \ \) A(3) \(\leftarrow \rightarrow\) C(1)
\(\ \ \ \ \ \ \ \) A(4) \(\leftarrow \rightarrow\) C(2)
\(\ \ \ \ \ \ \ \) A(5)
\(\leftarrow \rightarrow\)
C(3)
En la actualidad se la usa para apuntarla a variables de diferente
clase, por ejemplo un entero y una variable de caracter. Entonces puedo
poner en el entero por ejemplo el código ASCII en el entero como número
decimal y si se lo pide como caracter se puede ver ahora por su
representación en ese tipo de variables. Por ejemplo, si ponemos el
número 7 en una variable entera, pero esa variable también la veo como
una variable de caracteres, esa última me servirá para usarla como
código ASCII. Ya que el número se vería como texto pero en su
representación binaria. El código ASCII 7 es beep de las terminales.
Entonces, probemos hacerlo. Algunas terminales tienen bloqueado ese
ruido por molesto, así que puede ser que no lo escuchemos en la nuestra
(habría que mirar cómo está configurada en particular nuestro
terminal).
\(\ \ \ \ \ \ \ \)program
ruido
\(\ \ \ \ \ \ \ \)integer*2 bell
\(\ \ \ \ \ \ \ \)character*2 pip
\(\ \ \ \ \ \ \ \)equivalence(pip,bell)
\(\ \ \ \ \ \ \ \)bell=7
\(\ \ \ \ \ \ \ \)n=10
\(\ \ \ \ \ \ \ \)do i=1,n
\(\ \ \ \ \ \ \ \ \ \ \) write(*,*) pip,i
\(\ \ \ \ \ \ \ \ \ \ \) call system(’sleep 3 ’)
\(\ \ \ \ \ \ \ \)enddo
\(\ \ \ \ \ \ \
\)end
Si corro el programa escucho 10 beeps de la terminal, separados cada 3
segundos.
Facultad de Ciencias Astronómicas y Geofísicas - Universidad Nacional de La Plata.↩︎
El plural de mouse (ratón pero en este caso el animlito) es mice ya que es irregular en inglés, pero en el caso del ratón de las computadoras se ha aceptado mouses como el plural.↩︎
En la página web de la cátedra hay un apunte de como hacer esta instalación.↩︎
Existen lenguajes que se llaman de bajo nivel, en los cuales se programa a nivel de ordenes de la CPU.↩︎
En inglés: default, con esta palabra se indican las definiciones predeterminadas que ya se han adoptado, incluso en un sentido más amplio que sólo el tipo de variable.↩︎
Por ejemplo, en muchos sistemas la impresora es la Unidad Lógica Nº 6.↩︎
Se podría modificar esta sentencia y escribirla como suma = suma +1 /float(i)**2. la orden float convierte a flotante el número que está en i y evita el problema. Otra manera es convertir el 1 en 1. (el punto decimal lo convierte en número real y todas las operaciones que se realicen considerarán que los números son reales).↩︎
La mayoría de los compiladores construyen el código ejecutable de tal manera que haya un cero inicialmente en todas sus variables, por alguna razón misteriosa el gfortran no lo hace y debemos asignar un 0 a esta variable, ya que podría haber un valor en ella producto de lo que ha quedado en memoria de un programa anterior.↩︎
Default es una palabra anglosajona que se usa en computación para indicar valores que ya han sido predeterminados en el sistema. En este caso si yo no pongo paso por default el paso del DO es paso=1.↩︎
Atención: Este programa es muy ineficiente, ya que se repiten cálculos innecesariamente. Puede ser mejorado muy fácilmente, pero se volverá muy confuso y dejaría de tener utilidad con el fin de que sea un ejemplo. Se deja como ejercicio al lector el intentar mejorar su eficiencia, modificándolo para que realice la menor cantidad de cálculos posibles e igual arribe al resultado correcto.↩︎
Note que hemos asumido que \(0^0=1\) cuando esta operación da como resultado un valor indeterminado. Muchos lenguajes de computación (FORTRAN, Python, etc) consideran que el resultado es \(0^0=1\) por razones de simetría. Aunque este criterio puede ser discutible y no está generalizado a todos los lenguajes.↩︎
Recordar que en Fortran los números complejos se escriben como un par ordenado, con la siguiente estructura: (parte real, parte imaginaria)↩︎
Los fundamentes teóricos de porque una iteración funciona en un caso o en otro no es un tema del Análisis Numérico y existen maneras de asegurar la convergencia a una solución con este método↩︎
Algunos sistemas operativos permiten la sentencia INQUIRE que pregunta al sistema operativo el tamaño de renglón de un archivo directo↩︎
Microsoft, creadora del Windows, suele usar el símbolo \ para indicar los directorios↩︎
El sistema se encuentra con el caracter ASCII EOF (end of file) que sirve para indicar que el archivo llegó a su fin↩︎
Regla mnemotécnica: La suma extremos dividido dos más la suma de los puntos intermedios y todo esto multiplicado por el intervalo↩︎
Puede escribirse en un archivo aparte, pero debe compilarse con el programa que la utiliza. Ejemplo: gfortran programa.f funcion1.f funcion2.f -o programa.↩︎
En Fortran 90/95 es posible indicar variables que van ser modificadas por la subrutina, variables que no lo serán (inmutables), e incluso en variables que sólo tendrán los resultados de su ejecución. Pero esta facilidad es opcional y debe ser indicada explícitamente en el código.↩︎
A menos que se haya indicado alguna de ellas con el comando SAVE, que veremos más adelante↩︎
Veremos en este curso el libro Numerical Recipes, William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery, Este libro se puede consultar aquí↩︎
Puede no tener nombre, pero entonces no puedo poner más de una de estas sentencias↩︎